Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
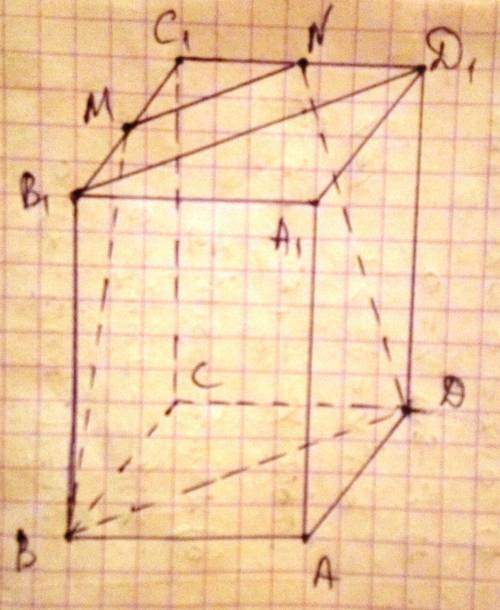
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
Висота буде 20 см
Объяснение:
Позначимо точки дотику на стороні ВС через Р , на стороні СД через К Сторона ВС складається з відрізківСК=4 см та КС =25 см , з точки С відходять дві дотичні прямі :СР та СК вони рівні і дорівнюють по 4 см.А з точки Д проходять дві дотичні прямі ДК та ДМ які теж однакові і дорівнюють по 25 см. З точки С проведемо висоту до основи АД і позначимо точку перетину через Ф .Якщо ДМ=25 см МФ=4 см , то ФД= 25-4=21 см. Трикутник СФД прямокутній , то можемо знайти висоту СФ
СФ²=СД²-ФД²=29²-21²=841-441=400√400=20 Висота СФ=20см