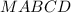 - правильная четырехугольная пирамида, около которой описан конус
- правильная четырехугольная пирамида, около которой описан конус 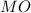 ⊥
⊥ 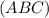
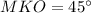
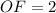 см
см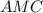 - осевое сечение конуса, где
- осевое сечение конуса, где 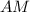 и
и 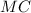 - образующие конуса
- образующие конуса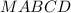 - правильная четырехугольная пирамида,
- правильная четырехугольная пирамида, 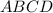
 ∩
∩ 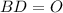
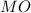 ⊥
⊥ 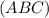
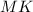 ⊥
⊥ 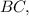 тогда
тогда 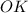 ⊥
⊥ 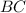 и
и 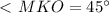 как линейный угол двугранного угла
как линейный угол двугранного угла  - центр окружности, описанной около квадрата
- центр окружности, описанной около квадрата  , т. е.
, т. е. 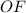 ⊥
⊥ 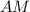
 тогда
тогда 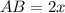
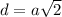 , где
, где 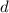 - диагональ квадрата,
- диагональ квадрата,  - сторона квадрата
- сторона квадрата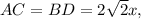 ( как диагонали квадрата)
( как диагонали квадрата)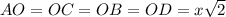
 - прямоугольный, равнобедренный, следовательно
- прямоугольный, равнобедренный, следовательно 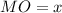
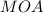 - прямоугольный
- прямоугольный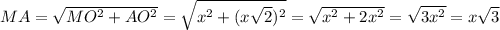
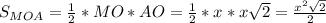 ,
,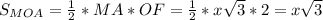
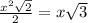
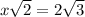
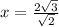
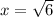
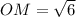 см
см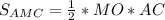
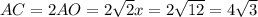 см
см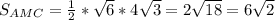 (см ²)
(см ²)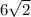 см²
см²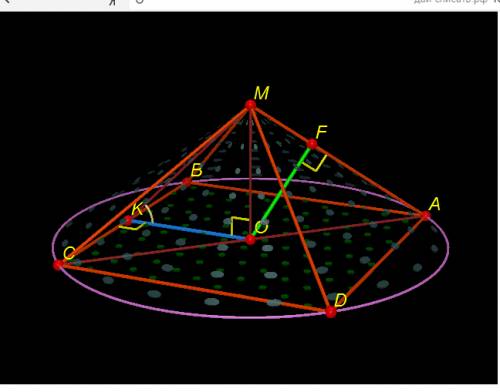
1)Через вершину С провести прямую параллельно диагонали.
Получится треугольник АСЕ,
в котором АЕ = 14+1=15м, АС = 13м, СЕ = 14м.
Найти площадь этого треугольника по формуле Герона.
Потом найти высоту этого треугольника, разделив две его площади на АЕ, то есть на 15.
Высота эта будет и высотой трапеции, площадь трапеции можно найти по формуле: S=1/2(a+b)h
2)Разность осн-ний=13см.
Высоты отсекают от большего осн-ния отрезки, один из кот. =х, другой=(13-х)
Выразив высоту трапеции через диагональ и часть большего осн-ния, получаем:
169-x^2=196-(13-x)^2
Найти "х", вычислить высоту (h)
Найти площадь по ф-ле: S=h*(a+b)/2=?