Объяснение:
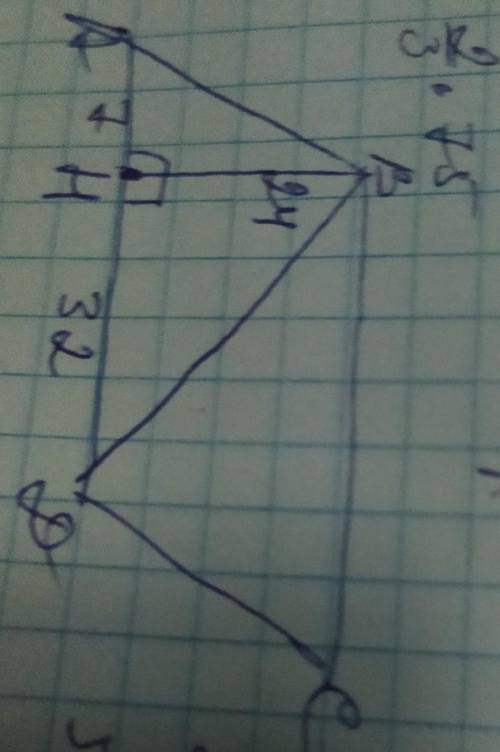
обозначим вершины параллелограмма А В С Д с высотой ВН и меньшей диагональю ВД. Высота ВН и диагональ ВД, образуют 2 прямоугольных треугольника АВН и ВДН, в которых ВН, АН, ДН - катеты, а АВ и ВД - гипотенузы. По теореме Пифагора найдём диагональ ВД в ∆ВДН:
ВД²=ВН²+АД²=24²+32²=576+1024=1600; ВД=√1600=40см
Также найдём АВ из ∆АВН:
АВ²=ВН²+АН²=24²+7²=576+49=625; АВ=√625=25см
АВ=СД=25см
АД=ВС=7+32=39см
Теперь найдём периметр параллелограмма зная его стороны: 2×25+2×39=50+78=128см
ОТВЕТ: Р=128 см, ВД=40см
Даны три вершины параллелограмма ABCD : A(-2;6;-9) , B( -12; 6;5) и C (4; 6; 5) . Найдите сумму координат вектора BD.
Объяснение:
" Для начала пояснение. Точка В получена параллельным переносом точки А. И точка С получена точно таким же параллельным переносом точки D на точку C.
Определим координаты вектора переноса ВА.
-12+2=-10
6-6=0
5+9=-14
То есть, осуществлен параллельный перенос на вектор ВА. Теперь
х(D)=4-(-10)=14 , у(D)=6-0=6 ,z(D)=5-14=-9⇒ D(14; 6; -9).
Координаты вектора BD(14-(-12) ; 6-6 ;-9-5) или BD( 26 ; 0 ;-14).
Сумма координат вектора BD такая 26+0+(-14)=12
9 1/3 см, 25 1/3 см, 25 1/3 см.
Объяснение:
Пусть основание х см, боковые стороны по х+16 см.
х+х+16+х+16=60
3х=28
х=9 1/3 см
Основание 9 1/3 см, боковые стороны по 9 1/3 + 16 = 25 1/3 см