Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Объяснение:
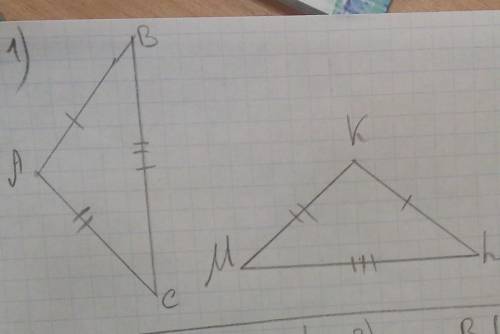
Дано: треугольник АВС и тррегольник KLM
AB=KL, BC=LM,AC=KM.
Доказать:ABC=KLM
Доказательство:
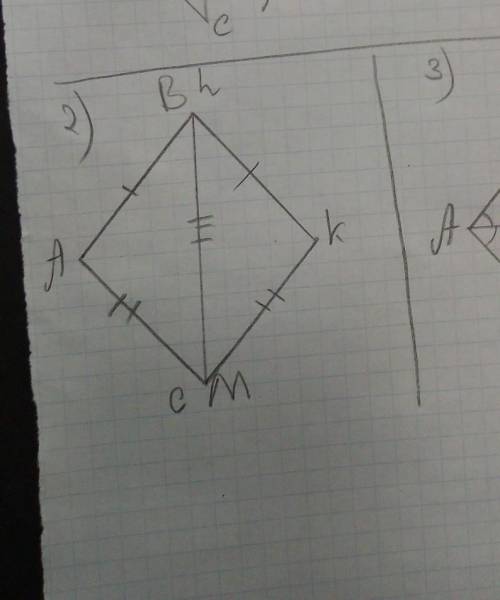
Совместим стороны треугольника, т.е. ВС и LM, т.к. по условию они равны друг другу следовательно совпадают.Вершины A и K находятся по разные стороны от общей стороны. Сторона AB симметрична равной ей стороне KL относительно общей стороны BC (LM). То же самое касается сторон AC и KM.
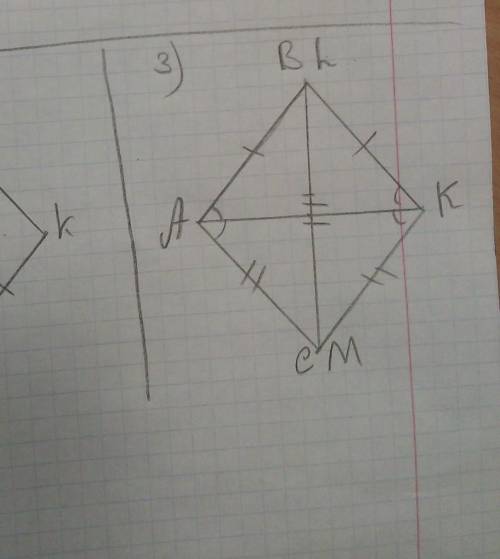
Проведём отрезок АК, у нас получатся два равнобедренных треугольника АКС(АС=КМ)и АКВ(АВ=KL).
В треугольниках ABC и KLM соответственно равны стороны AB и KL, AC и KM (по условию задачи). И как мы выяснили, угол A равен углу K.
В треугольниках ABC и KLM соответственно равны стороны AB и KL, AC и KM (по условию задачи). И как мы выяснили, угол A равен углу K.В соответствии с первым признаком равенства треугольников, если у них равны две стороны и угол между ними, то такие треугольники равны. Значит ∆ABC = ∆KLM.
В треугольниках ABC и KLM соответственно равны стороны AB и KL, AC и KM (по условию задачи). И как мы выяснили, угол A равен углу K.В соответствии с первым признаком равенства треугольников, если у них равны две стороны и угол между ними, то такие треугольники равны. Значит ∆ABC = ∆KLM.Таким образом третий признак равенства треугольников был доказан.
1.1.
Если прямая не находится в плоскости, то она может пересекать её или быть параллельной ей. Тогда плоскости могут пересекатся или быть параллельными, последнее далеко не всегда верно, но этому ни чего не противоречит, по условию, так что это возможно.
ответ: б) параллельны или пересекающиеся.
1.2.
По признаку параллельности прямой и плоскости - мы имеем множество прямых, которые параллельны второй плоскости и они лежат в первой плоскости эта плоскость так же параллельна второй плоскости, ведь если она пересечёт, то найдётся такая прямая, которая так же пересечёт, а как мы выянили все прямые параллельны.
ответ: б) параллельны.
2.
По определению скрещивающиеся прямые это такие прямые, которые не находятся в одной плоскости. Пересекающиеся прямые всегда лежат в одной плоскости (одно из следствий из одной аксиомы стереометрии). Прямые параллельны в пространстве, если они лежат в одной плоскости и не пересекаются (определение).
2.1.
ответ: а) скрещивающиеся.
2.2.
ответ: в) параллельны или пересекающиеся.
Объяснение: