
 =
=
 см
см
ЗАДАНИЕ 1
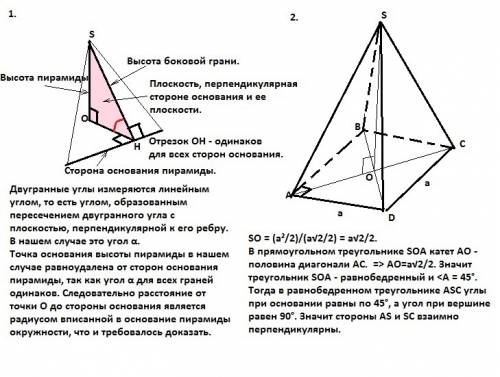
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.
Проведем через вершину пирамиды S плоскости, перпендикулярные ребрам двугранных углов пирамиды, то есть плоскости, перпендикулярные сторонам основания пирамиды и, следовательно, перпендикулярные самому основанию.
Тогда у всех этих плоскостей имеются две общие точки: вершина пирамиды S и ее проекция на основание пирамиды точка О. То есть эти плоскости пересекаются по прямой SO, являющейся высотой пирамиды. Линии пересечения этих плоскостей и пирамиды - это высота боковой грани и перпендикуляр из точки О основания высоты пирамиды к стороне основания пирамиды. Этот перпендикуляр - проекция высоты боковой грани на плоскость основания и в силу равенства двугранных углов (дано) одинаков для всех проведенных плоскостей, так как тангенс этих углов равен отношению высоты пирамиды к проекции высоты боковой грани. Итак, точка основания высоты пирамиды в нашем случае равноудалена от сторон основания пирамиды, следовательно, расстояние от этой точки до стороны основания пирамиды является радиусом вписанной в основание пирамиды окружности, что и требовалось доказать.
ЗАДАНИЕ 2.
Основание правильной пирамиды SABCD - квадрат ABCD со стороной "а". Его площадь равна а². Значит площадь диагонального сечения равна а²/2 (дано). Диагональное сечение правильной пирамиды - равнобедренный треугольник ASC с основанием - диагональю квадрата, равной а√2. Площадь диагонального сечения S=(1/2)*АС*SO (SO - высота пирамиды). Итак, (1/2)*а√2*SO = а²/2. Тогда
SO = (а²/2)/(а√2/2) = a√2/2. В прямоугольном треугольнике SOA катет АО - половина диагонали АС. АО=a√2/2. Значит треугольник SOA - равнобедренный и <A = 45°. Тогда в равнобедренном треугольнике ASC углы при основании равны по 45°, а угол при вершине равен 90°. Значит стороны AS и SC взаимно перпендикулярны.
AS и SC - противоположные ребра пирамиды. Они перпендикулярны. Что и требовалось доказать.
ВД^2+ДС^2=ВС^2
ВД^2=ВС^2-ДС^2=169-144=25
ВД=5см высота
уголА=углу АВД=45, отсюда следует что АВД равнобедренный и
АД=АВ=5см. АС=5+12=17см
S АВС=1/2АС*ВД=1/2*17*5=42,5кв.см