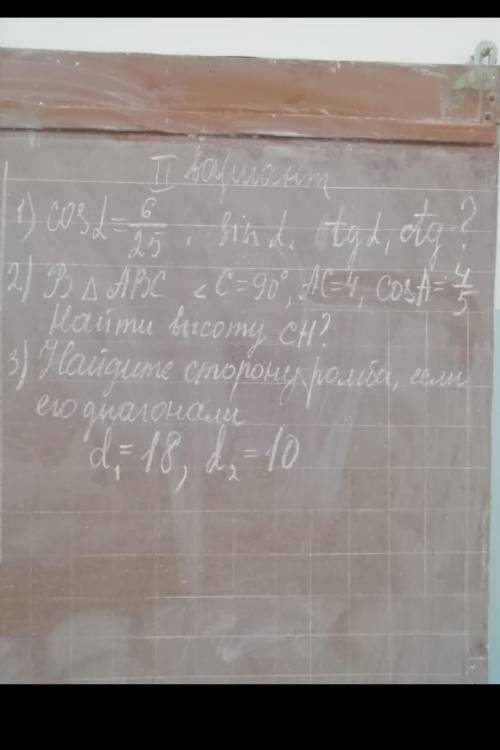
Объяснение: в треугольнике с 30,60,90 есть такое свойтво наименьший катет А(противолежит углу 30 ) а другой катет (протеволежит углу 60 )A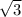
а гипотенуза равна 2A так вот в 4 задаче так и выходит СD=3,5 AD=7 и AC=3,5 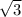тогда исходя из свойства угол D=60гр так как противолежит AC , так как СB=CD исходя из того что AC общая высота и для ACD и ABC то треугольник ABC равносторонний и угол В=60 5) тут аналогично используем тоже самое свойство уголs KPC=30 ; PKC=60 ;CKE=30;CEK=60 тогда СE=4,5 так как противолежит углу в 30гр и СK=4,5 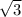; а PC=CK* = 
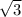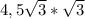=13,5 ответ CE=4,5 PC=13,5 если вам интересно откуда взялось это свойство то почитайте в интернете свойства треугольника с 30,60,90 градусами
На сторонах угла∡ABC точки A и C находятся в равных расстояниях от вершины угла BA=BC. Через эти точки к сторонам угла проведены перпендикуляры AE⊥BA CD⊥BC.
1. Чтобы доказать равенство ΔAFD и ΔCFE, докажем, что ΔBAE и ΔBCD, по второму признаку равенства треугольников:
BA=BC
∡BAF=∡BCF=90°
∡ABC — общий.
В этих треугольниках равны все соответсвующие эелементы, в том числе BD=BE, ∡D=∡E.
Если BD=BE и BA=BC, то BD−BA=BE−BC, то есть AD=CE.
Очевидно равенство ΔAFD и ΔCFE также доказываем по второму признаку равенства треугольников:
AD=CE
∡DAF=∡ECF=90°
∡D=∡
Подробнее - на -
Объяснение: