ответ: 2 см и 10 см
Объяснение:
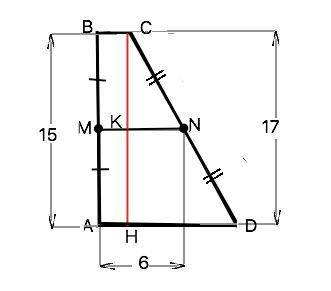
Обозначим трапецию АВСD. ВС║АD, АВ=15 см, СD=17 см, ВC⊥АB
Трапеция прямоугольная, ⇒ высота CH трапеции параллельна и равна меньшей боковой стороне. СН=АВ=15 см. Отношение сторон треугольника СHD из Пифагоровых троек (8:15:17), ⇒ НD=8 см ( проверьте по т.Пифагора) Т.к.MN средняя линия трапеции, отрезок КN - средняя линия треугольника СНD, поэтому по свойству средней линии КN=HD:2=8:2=4 см.
АВСН - прямоугольник ( что легко доказывается). ⇒
BC=АН=MN-KN=6-4=2 см и АD=AH+HD=2+8=10 см.
Косинус угла - это отношение прилежащего катета к гипотенузе
cos A = AC/AB
AC = BC = AB * cos45 = 4√2 см.
С прямоугольного треугольника CDA ( угол ADC = 90 градусов)
Синус угла - это отношение противолежащего катета к гипотенузе:
sin A = CD/AC
CD = AC*sin 45= 4√2*1/√2= 4 см
ответ: СD = 4 см.