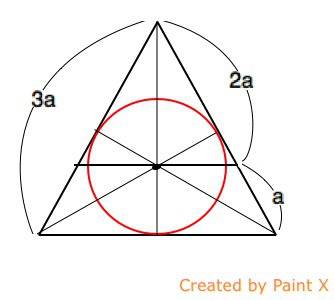
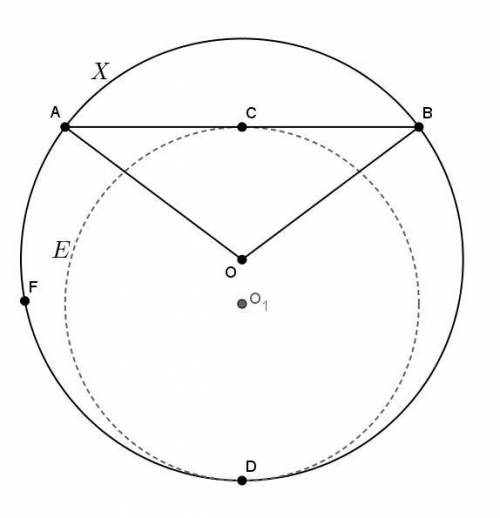
См. рисунок.
Обозначим центр малой окружности через 
. Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке: 
.
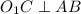Если отрезок перпендикулярен хорде, то при их пересечении он делит хорду пополам (это теорема, которую изучают в школе). Значит, точка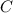 
— середина хорды 
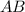. Треугольник 
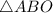равнобедренный (поскольку отрезк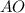и 
и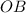 
равны как радиусы). Значит, медиана 
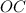является также и высотой. Получим, что 
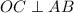. Учитывая предыдущее равенство, получим, что 
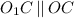. Это значит, что точки 
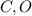и лежат на одной прямой. Тогда на той же прямой лежит точка касания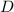 
(ведь по условию она диаметрально противополож
одно любое ребро будет перпендикулярно 2-м граням