Объяснение:
12
Если диагональ образует с площадью основания,то диагональ основания равна высоте прямоугольного параллелепипеда.
Найдём диагональ основания по теореме Пифагора:
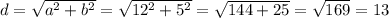
h=d=13 см
S = 2(a · b + a · h + b · h)=2(12 · 5 + 12 · 13 + 5 · 13) =2(60+156+65) = =2*281=562 см²
V=a · b · h=12 · 5 · 13=780 см³
13
Если образующая конуса наклонена к плоскости основания на 45°,то радиус основания равен высоте.Примем радиус основания за х,тогда по теореме Пифагора:
l²=2r²
12²=2x²
x²=144:2
x²=72
x=√72=6√2 см
S=π r (r + l)=π6√2(6√2+12)=π72+π72√2=π72(1+√2) см²
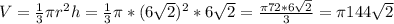
V=144√2 π см³
находим площади треугольников по формуле герона:
S=rad(p(p-a)(p-b)(p-c))
rad-корень
p-полупериметр
a,b,c-стороны треугольника
1)Находим полупериметр:
(формула: p=(a+b+c)/2)
полупериметр первого треугольника:
p=(5+8+12)/2
p=12,5cm
полупериметр второго треугольника:
p=(15+24+36)/2
p=37,5cm
2)Находим площадь:
площадь первого треугольника:
S1=rad(12,5(12,5-5)(12,5-8)(12,5-12))
S1=rad(12,5×7,5×4,5×0,5)
S1=(15rad15)4
площадь второго треугольника:
S2=rad(37,5(37,5-15)(37,5-24)(37,5-36))
S2=rad(37,5×22,5×13,5×0,5)
S2=(135rad5)/4
3)Находим отношение площадей:
S1/S2=((15rad15)/4)/((135rad5)/4)
S1/S2=(rad3)/9