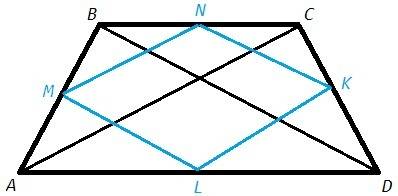
Середины сторон четырехугольника являются вершинами параллелограмма (теорема Вариньона). Стороны параллелограмма Вариньона параллельны диагоналям четырехугольника и равны их половинам (т.к. являются средними линиями в треугольниках, образованных сторонами и диагоналями).
Диагонали равнобедренной трапеции равны, следовательно стороны параллелограмма Вариньона равны и он является ромбом.
MN - средняя линия в ABC => MN||AC, MN=AC/2. Аналогично LK||AC, LK=AC/2.
MN||LK, MN=LK => MNKL - параллелограмм (противоположные стороны параллельны и равны).
AC=BD, NK=BD/2 => MN=NK => MNKL - ромб (смежные стороны равны).
1) Для начала надо решить эту задачу, а затем поделить ответы на 2 и всё сложить.
3х - 1 сторона.
4х - 2 сторона.
5х - 3 сторона.
48 см - Р данного треугольника.
Составим и решим уравнение:
3х+4х+5х = 48;
12х = 48;
х = 4.
3×4=12 (см) - 1 сторона.
4×4=16 (см) - 2 сторона.
5×4=20 (см) - 3 сторона.
1.12÷2 = 6 - середина 1 отрезка.
2.16÷2 = 8 - середина 2 отрезка.
3.20÷2 =10. - середина 3 отрезка.
4.6+8+10 = 24 - Р треуг., вершины которого равны середине сторон.
ответ: 24.
2) Вообще, можно просто поделить Р первого данного нам треугольника на 2, то бишь:
48÷2 = 24.
ответ: 24.
Но Вам мой совет, если Вы всё-таки спросили это для домашней работы, думаю, лучше всё-таки использовать первый вариант.