ответ: 81 см см³
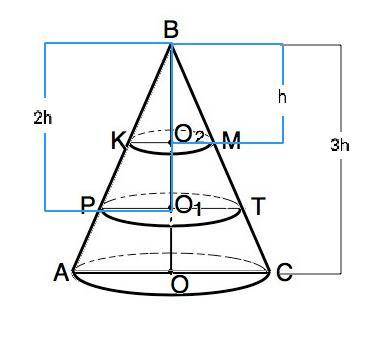
Объяснение: Конус сечениями, параллельными основанию, делится на три подобных фигуры. Высота меньшего –1/3 высоты исходного. а высота среднего –2/3 высоты исходного. (см. рисунок).
Отношение объемов подобных фигур равно кубу коэффициента отношения их линейных размеров. Рассмотрим меньший и средний конус: k=h:2h=1/2 ⇒ V(KВM):V(PВT)=k³=1/8.=> объем средней части (усеченного конуса)=8-1=7V (КВМ), тогда объем меньшего (верхнего) конуса равен 21:7=3 см³ Отношение высоты исходного конуса к высоте меньшего k=3:1, следовательно, k³=27. Объем исходного конуса 27•3=81 (см³)
2)Проведем из вершины C высоту CH1 к стороне AD, затем AH и H1D обозначим буквой x, они будут являться катетами прямоугольных треугольников ABH и CH1D.
3)Составим уравнение AD=BC+2x, т.к. HH1=BC
2x=AD-BC
x=21
4) Рассмотрим треугольник ABH:
AB=29( по условию);
AH=21( по доказанному);
AB^2= AH^2+BH^2
BH^2=841-441
BH=20
5)S= 0.5* ( 7+49) * 20
S=560
ответ: 560