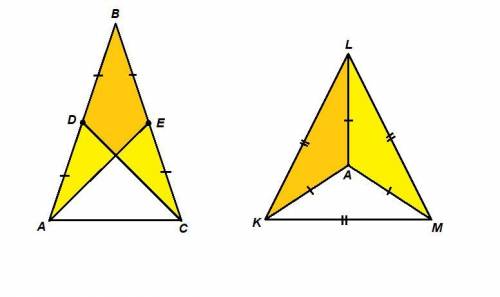
1) Дано: ΔАВС, D - середина АВ, Е - середина ВС, AD = CE.
Доказать: ΔBDC = ΔBEA.
Доказательство:
AD = DB, так как D - середина АВ,
СЕ = ЕВ, так как Е - середина ВС,
AD = CE по условию, значит
AD = DB = СЕ = ЕВ, а следовательно
АВ = ВС.
В треугольниках BDC и BEA:
ВС = АВ,
DB = EB,
∠B - общий, ⇒
ΔBDC = ΔBEA по двум сторонам и углу между ними.
2) Дано: ΔKLM - равносторонний, А - внутренняя точка ΔKLM,
AK = AL = AM.
Доказать: ΔKLA = ΔMLA.
Доказательство:
АК = АМ по условию,
LK = LM как стороны равностороннего треугольника,
AL - общая сторона для треугольников KLA и MLA, ⇒
ΔKLA = ΔMLA по трем сторонам.
Отрезок МК=6 не пересекает плоскость.
Концы отрезка МК удалены от плоскости на 8√3 и 5√3.
Найти угол между прямой МК и плоскостью.
Угол между прямой и плоскостью - угол между прямой и ее проекцией.
Спроециуем отрезок MK на плоскость - опустим перпендикуляры MM1 и KK1.
Расстояние от точки до плоскости измеряется длиной перпендикуляра.
По условию MM1=8√3, KK1=5√3.
Теперь найдем угол между прямой MK и ее проекцией M1K1.
В плоскости опущенных перпендикуляров проведем TK || M1K1.
TM1=KK1=5√3, MT=8√3-5√3=3√3
В треугольнике MKT
sin(MKT) =MT/MK =3√3/6 =√3/2 => ∠MKT=60° (острый)
∠(MK, M1K1) =∠MKT =60°