Question

ІВ, БУДУ ВДЯЧНА ЗА ДО !!""♡ (Известно, что |а| = 2, |б| = 3, |а + б| =√19. Вычислите:
а) Угол между векторами а и б;
б) |2а - б|)

Answer 1

Известно, что |а| = 2, |b| = 3, |а + b| =√19. Вычислите:

а) Угол между векторами а и b;  б) |2а - b| .

Объяснение:

a)По правилу  параллелограма суммой векторов a и b будет $\displaystyle \vec{AC}= \vec{a} + \vec{b}$. Значит  $\displaystyle |\vec{AC} | =| \vec{a} + \vec{b}|=\sqrt{19}$

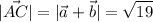
Пусть α угол между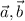  $\displaystyle \vec{a} , \vec{b}$ .Тогда ∠АВС=180°-α

ΔАВС, по т косинусов

АС²=АВ²+ВС²-2*АВ*ВС*cos(180-α)

19=4+9-2*2*3*(-cosα),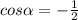   $cos\alpha =-\frac{1}{2}$   , α=120°

б) Угол между векторами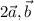 $\displaystyle 2 \vec{a} , \vec{b}$ равен 120° , тк эти вектора соноправлены  с векторами $\displaystyle \vec{a} , \vec{b}$ .

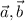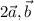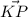Разностью векторов  $\displaystyle 2 \vec{a} , \vec{b}$ будет $\displaystyle \vec{KP}$  Найдем его длину из ΔОРК по теореме косинусов  КР²=ОР²+ОК²-2*ОР*ОК*cos∠РОК ,

КР²=4²+3²-2*4*3*cos120° ,

КР²=16+9-24*(-0,5) ,  КР=√37.