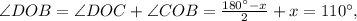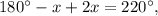ответ:1. Если KM = NJ, ML = JR, __М= J__, то ΔKML=ΔNJR по первому признаку- по двум сторонам и углу между ними
2. KM = NJ, ML = JR,_KL=NR_, то ΔKML=ΔNJR по третьему признаку-по трем сторонам.
3. KL = NR, ∡ K = ∡ N, _∡ L= ∡ R, то
ΔKML=ΔNJR по второму признаку-по стороне и двум прилежащим углам.
4. KL = NR, ∡ K = ∡ N,_KM=NJ__ , то ΔKML=ΔNJR по первому признаку- по двум сторонам и углу между ними
5. ∡ M = ∡ J, ∡ L = ∡ R, _ML =NR_ , то ΔKML=ΔNJR по второму признаку-по стороне и двум прилежащим углам.
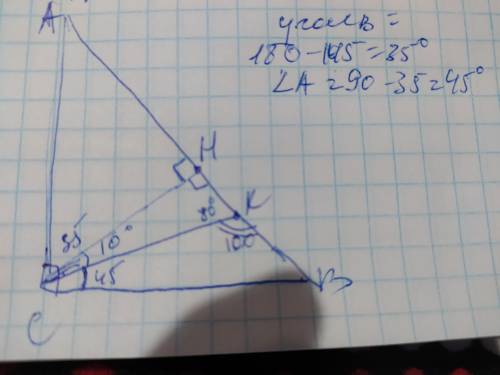
ответ: угол А=45°, угол В=35°
Объяснение: обозначим вершины треугольника А В С, где угол С=90°, высоту–СН, биссектрису СК. Так как биссектриса делит угол С пополам то угол КСВ=45°. Рассмотрим полученный ∆СНК. Он прямоугольный: угол СНК=90°; угол КСН=10°, так как сумма острых углов прямоугольного треугольника составляет 90°, то угол СКН=90-10=80°. Теперь рассмотрим полученный ∆КВС. Угол СКВсмежный с углом СКН и так как сумма смежных углов составляет 180°, то
угол СКВ=180-80=100°. Также в этом треугольнике мы нашли угол КСВ=45°. Так как сумма углов треугольника составляет 180°, то
угол В=180-100-45=35°. Теперь найдём угол А. Угол А=90-35°=45°
4.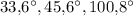
6. а)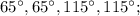 б)
б) 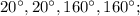 в)
в) 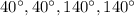
7.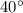
Объяснение:
4. Путь первый из полученных углов равен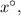 тогда второй равен
тогда второй равен 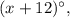 а третий равен
а третий равен 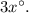 Так как вместе они составляют развернутый угол, то
Так как вместе они составляют развернутый угол, то 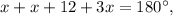
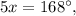
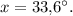
Образованные углы равны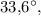
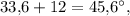
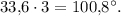
6. При пересечении двух прямых образуются две пары равных углов (или четыре равных прямых угла). Рассматривая пару смежных углов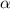 и
и 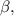 сумма которых равна
сумма которых равна 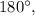 получаем:
получаем:
а)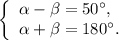
Складывая полученные уравнения, находим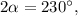
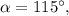 откуда из второго уравнения
откуда из второго уравнения 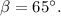
б)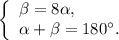
Подставляя значение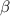 из первого уравнения во второе, находим
из первого уравнения во второе, находим 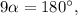
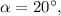 откуда
откуда 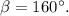
в) Так как сумма пары смежных углов равна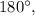 речь идет о паре острых вертикальных углов,
речь идет о паре острых вертикальных углов, 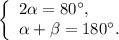
Из первого уравнения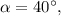 тогда из второго
тогда из второго 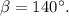
7. Пусть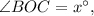 тогда
тогда 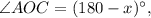 а его половина
а его половина 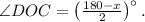 Значит
Значит