У рівнобедрений трикутник вписано квадрат одиничної площі, одна сторона якого лежить на основі трикутника. Знайти площу трикутника, якщо відомо, що центри мас трикутника і квадрата збігаються ( центр мас трикутника лежить на перетині його медіан).
Проведем диагонали квадрата. Они пересекутся в точке , которая является центром масс треугольника . Так как это точка пересечения медиан, то точка разбивает медиану в отношении считая от вершины. Учитывая, что равно половине стороны квадрата, а сторона квадрата по условию равна 1, то
Так как , где то
Таким образом, треугольники и подобны с коэффициентом
Пусть у нас есть отрезок AB. Считаем, что он расположен в 1-й четверти координатной сетки и не параллелен осям координат (прочие положения отрезка рассматриваются аналогично). Координаты концов отрезка: A(x₁, y₁) и B(x₂, y₂). Допустим, что x₂>x₁. Пусть C - середина отрезка AB с координатами (x, y). Требуется выразить x и y через координаты точек A и B.
Определение координаты x. Из точек A, B и C отпустим перпендикуляры на отрезок OX, точки пересечения с осью OX обозначим A₁, B₁ и C₁.
AA₁⊥OX BB⊥OX CC⊥OX
Т.к. C - середина отрезка AB, то AC=BC. Т.к. AA₁||BB₁||CC₁, то по теореме Фалеса A₁C₁=B₁C₁. Значит, C₁ - середина отрезка A₁B₁.
Координаты точки A₁ равны (x₁;0). Координаты точки B₁ равны (x₂;0). Координаты точки C₁ равны (x;0).
Длина отрезка A₁C₁ равна x-x₁. Длина отрезка B₁C₁ равна x₂-x.
Эти длины равны, т.е. x-x₁=x₂-x ⇔ 2x=x₁+x₂ ⇔ x = (x₁+x₂) / 2.
Т.о., координата x середины отрезка есть полусумма координат x концов отрезка.
Определение координаты y. Выполняется аналогично, выполняя проекцию отрезка AB на координатную ось OY. y = (y₁+y₂) / 2
Т.о., координаты середины отрезка AB есть полусумма соответствующих координат концов отрезка.
1) Пусть a и b - два данных вектора. Если вектор р представлен в виде p=xa+yb, где х и у -некоторые числа, то говорят, что вектор р разложен по векторам a и b. Числа х и у называются коэффициентами разложения.
2) Отложим от точки О два единичных вектора, направление которых совпадает с направлениями координатных осей. Эти векторы обозначаются i и j и называются координатными векторами. Так как координатные вектора не коллинеарны, то любой вектор р можно представить в виде p=xi+yj. Числа х и у называются координатами вектора в данной системе координат. Для координат векторов справедливы следующие свойства: 1. Каждая координата суммы векторов равна сумме соответствующих координат. 2. Каждая координата разности векторов равна разности соответствующих координат. 3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. 4. Каждая координата вектора равна разности соответствующих координат его конца и начала.
Площадь треугольника равна 2,25
Объяснение:
Проведем диагонали квадрата. Они пересекутся в точке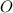 , которая является центром масс треугольника
, которая является центром масс треугольника 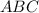 . Так как это точка пересечения медиан, то точка
. Так как это точка пересечения медиан, то точка 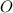 разбивает медиану
разбивает медиану 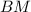 в отношении
в отношении 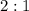 считая от вершины. Учитывая, что
считая от вершины. Учитывая, что 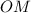 равно половине стороны квадрата, а сторона квадрата по условию равна 1, то
равно половине стороны квадрата, а сторона квадрата по условию равна 1, то
Так как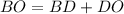 , где
, где 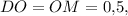 то
то
Таким образом, треугольники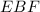 и
и 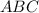 подобны с коэффициентом
подобны с коэффициентом 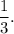
Тогда