1. Вспомним признак прямоугольника: если в четырёхугольнике три угла равны по 90°, то этот четырёхугольник - прямоугольник. Рассмотрим и проверим этот признак в данной задаче:
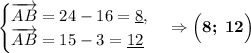
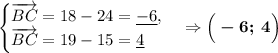
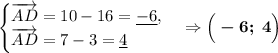
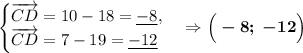
Вспомним свойство о скалярном произведении векторов: если произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны. Найдём такие пары векторов:
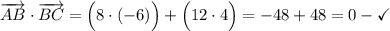
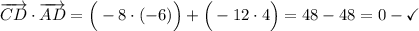
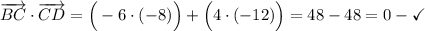
Теперь мы можем утверждать, что фигура "ABCD" - прямоугольник, т.к. углы "B", "C" и "D" составляют по 90° каждый.
Что и требовалось доказать.
2. Площадь прямоугольника - произведение его длины и ширины. Поэтому сначала нужно найти, чему равна длина и ширина.
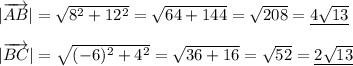
Теперь, когда нам известна и длина, и ширина, найдём площадь прямоугольника:
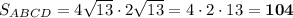 см².
см².
ответ: 104 см².
Объяснение:
ё1)Дан треугольник ABC A(6;0), B(6;8) и C(3;4).
Определи AB = ; BC = ; AC =
Треугольник ABC
равнобедренный ? разносторонний ? равносторонний?
Решение.
АВ=√(6-6)²+(8-0)²=√(0+64)=8
ВС=√(3-6)²+(4-8)²=√(9+16)=√25=5
АС=√(3-6)²+(4-0)²=√(9+16)=√25=5. Две стороны равны ,значит треугольник равнобедренный .
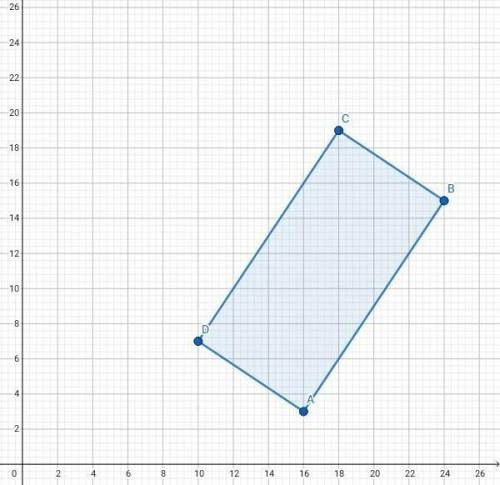
2)ABCD-прямоугольник,A(16;3), B(20;7), C(18;9) и D(14;5). Найти S.
Решение. ABCD-будет прямоугольником если противоположные стороны равны +диагонали равны.
АВ=√(20-16)²+(7-3)²=√(16+16)=4√2,
ВС=√(4+4)=2√2,
СD=√(16+16)=4√2,
DА=√(4+4)=2√2, Т.о. АВ=СD , ВС=DА и Оп четырехугольник превращается в параллелограмм.
АС=√(4+36)=2√10,
ВD=√(36+4)=2√10.И Оп параллелограмм. превращается в прямоугольник.
Площа бічної поверхні циліндра обчислюється за формулою:
S біч. = h * π * d
де h - висота циліндра, d - діаметр циліндра.
Оскільки діаметр дорівнює 6 см, то радіус дорівнює 3 см (6/2), а довжина осьового перерізу може бути знайдена за теоремою Піфагора:
d² = 2r²
10² = 2 * 3²
100 = 18
Отже, довжина осьового перерізу дорівнює √18 см.
Тоді за формулою:
S біч. = h * π * d
S біч. = h * π * 6
Будемо шукати h за до вимірювання висоти на малюнку:

h = АВ = АД - ВД = √18 - 3 = √18 - √9 ≈ 1.73 см.
Тоді площа бічної поверхні циліндра:
S біч. = h * π * d
S біч. = 1.73 * 3.14 * 6 ≈ 32.70 см².
Отже, площа бічної поверхні циліндра становить близько 32.70 см².