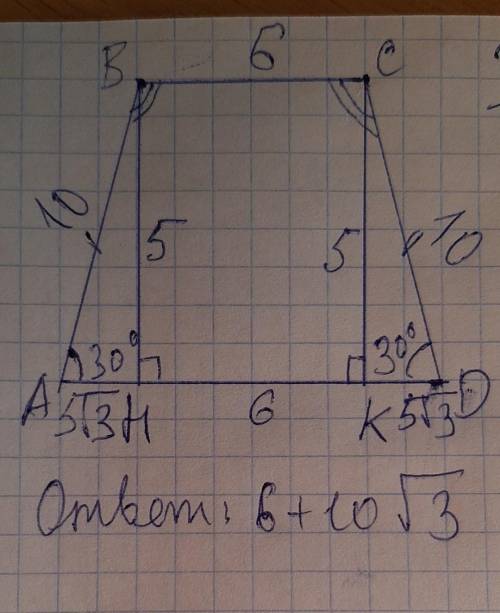
Решение: Проведём высоту СК.
Значит, BHKC прямоугольник, тогда ВС=HK=6 , BH=CK=5.
В треугольнике АВН угол АНВ= 90°, значит треугольник АВН - прямоугольный, т.к. угол А=30° и катет ВН=5, то гипотенуза АВ= 10 ( т.к. в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы).
Т.к. АВСD - равнобедеренная трапеция, то угол А = углу D = 30°.
Значит треугольник АВН= треугольнику СКD (по гипотенузе и острому углу)
Треугольнике АВН - прямоуольный:
По теореме Пифагора:
АН² + ВН²= АВ²
АН² = АВ² - ВН²
АН² = 100 - 25 = 75
АН = корень в квадрате из 75 = 5 корней из трёх
АН = КD = 5 корней из трёх
АD = 6 + 5 корней из трёз + 5 корней из трёх = 6 + 10 корней из трёх.
ответ: 6 + 10 корней из трёх.
Треугольники ACO и BCO - прямоугольные (по свойству касательной).
То есть углы CAO и CBO равны по 90° каждый.
OC - является биссектрисой для угла ACB (по свойству касательных), следовательно углы ACO и BCO равны 6°/2=3°.
По теореме о сумме углов треугольника, для треугольника ACO запишем:
180°=∠OAC+∠ACO+∠COA
180°=90°+3°+∠COA
∠COA=180°-90°-3°=87°
Аналогично, для треугольника BCO получим, что ∠COB=87°
∠AOB=∠COA+∠COB=87°+87°=174°
Проведем отрезок AB и рассмотрим треугольник ABO.
По теореме о сумме углов треугольника запишем:
180°=∠AOB+∠BAO+∠ABO
180°=174°+∠BAO+∠ABO
∠BAO+∠ABO=6°
ABO равнобедренный треугольник, т.к. OA и OB - радиусы окружности и, поэтому, равны. Следовательно ∠ABO=∠BAO (по свойству равнобедренного треугольника). И получается, что ∠ABO=∠BAO=6°/2=3°
ответ: ∠ABO=3°