В основании пирамиды лежит правильный треугольник со стороной 5 см. Основание высоты Пирамиды равноудалено от сторон этого треугольника. Высота одной из боковых граней равна 10 см. Вычислить боковую поверхность пирамиды.
Объяснение:
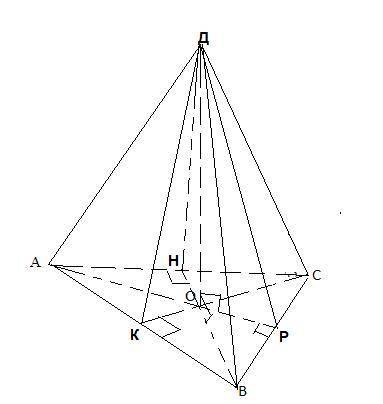
АВСД-пирамида, ДО-высота пирамиды .Пусть ДК⊥АВ, ДР⊥ВС, ДН⊥АС.
Т.к. О-основание высоты пирамиды равноудалено от сторон треугольника, то О-центр вписанной окружности и расстояние от О до стороны треугольника это r-вписанной окружности.
Тогда высоты всех боковых граней(т.е апофемы ) равны, т.к прямоугольные ΔДОК=ΔДОР=ΔДОН по двум катетам ДО-общая, ОК=ОР=ОН=r.
S(бок.)=1/2*Р(осн.)*а , где а-апофема .
Р=3*5=15 (см).
S(бок.)=1/2*15*10=75 (см²)
Радиус окружности, описанной около равнобедренного треугольника с углом 120°, равен см. Найдите стороны треугольника
Объяснение:
ΔАВС, ∠В=120°, О-центр описанной окружности. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров к его сторонам.
Пусть ВН⊥АС, О∈ВН., ОВ=ОА=6√3 см.
По теореме синусов( отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности) :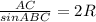 
, 
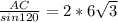, АС=12√3*
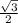=18 (см).
По свойству высоты равнобедренного треугольника ∠АВН=∠НВС=60°, АН=НС=9 см.
ΔАВН-прямоугольный , sin 60°=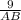
, АВ=6√3 см ⇒ВС=6√3 см.
1) внутрішній дотик
2) кола перетинаються
3) не мають спільних точок
Объяснение:
1)
d=6см
R-r=8-2=6см
d=R-r, внутрішній дотик
2)
d=6см
R+r=5+3=8см
6<8
d<R+r, кола перетинаються
3)
d=6см
R+r=2+3=5см
6>5
d>R+r, кола не мають спільних точок.