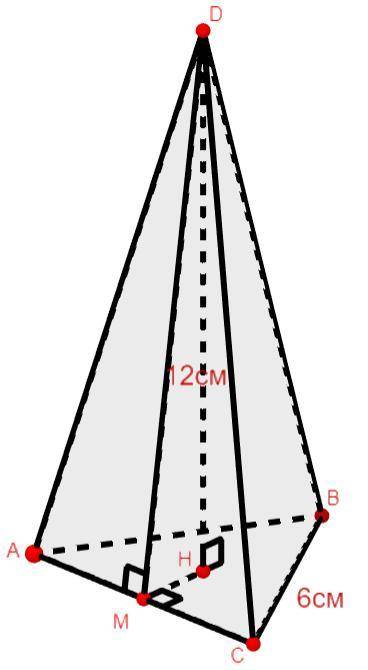
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
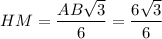=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
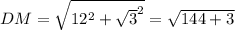=√147 см
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
тут так
точки L,K,M,N центра сторон AB,BC,CD,DA соответственно.
рассмо треугольник abc
LK соединяет центры, значит это средняя линия треугольника.
рассмо треугольник acd
mn - средняя линия
средние линии параллельны основаниям треугольников, в данном случае диагоналям 4-хугольника.
значит kl=MN и плюс параллельны получается что это фигура параллелограм
так как стороны параллельны диагоналям получаем что диагонали взаимно перпендикулярны а дальше что площадь равна
s=d1*d2/2=10*14/2=70 - ответ