1) 9 целых 1/16 - (5/8 + 7/16) = в голове делаем общий знаменатель в скобках, получается 9 целых 1/16 - 1/16 = 8
2) 3 целых 7/8 - (2 целых 3/8 - 1 целая 3/4) = общий знаменатель к неправильным дробям в скобках и получается 3 целых 7/8 - 5/8 = 3 целых 2/8
3) 7 целых 3/4 + (2 целых 7/8 - 1 целая 3/4) = общий знаменатель в скобках и получается 7 целых 3/4 + 1 целая 1/8 = 8 целых 7/8
4) 3 целых 1/2 * 2 + 2 целых 1/2 * 2 + 3 целых 1/2 * 2 = 6 целых 1/2 + 4 целых 1/2 + 6 целых 1/2 = 16 целых 3/2 = 17 целых 1/2
Объяснение:
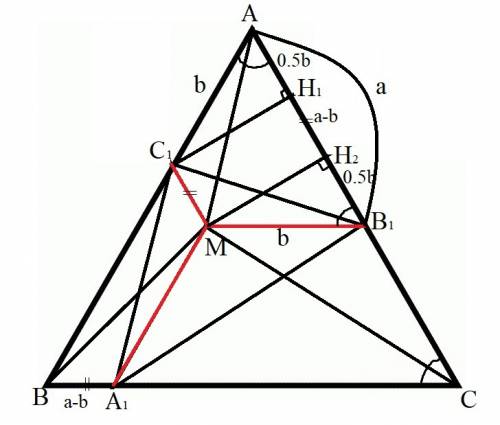
Пусть MA₁║AB, MB₁║BC, MC₁║AC.
Рассмотрим фигуру AB₁MC₁. Т. к. MC₁║AC ⇒ MC₁║AB₁, AC₁∦MB₁ ⇒ AB₁MC₁ - трапеция. Т. к. ∠A = ∠C, ∠C = ∠AB₁M как соответственные ⇒ ∠A = ∠AB₁M ⇒ AC₁ = MB₁, т. е. трапеция равнобедренная ⇒ B₁C₁ = AM как диагонали равнобедренной трапеции.
Аналогично рассуждая, C₁A₁ = BM, A₁B₁ = CM, что и требовалось доказать.
Пусть C₁H₁⊥AB₁, MH₂⊥AB₁. Тогда MC₁H₁H₂ - прямоугольник ⇒ H₁H₂ = C₁M. Т. к. A₁BC₁M - равнобедренная трапеция, A₁B = C₁M ⇒ A₁B = H₁H₂.
В прямоугольном треугольнике AH₁C₁ AH₁ = AC₁ * cos A = b * cos 60° = 0.5b. Аналогично B₁H₂ = 0.5b. Тогда H₁H₂ = AB₁ - AH₁ - H₂B₁ = a - 0.5b - 0.5b = a - b ⇒ A₁B = a - b.
ответ: a - b