К сожалению, в задании не сказано, как расположен этот угол.
Даю 2 варианта:
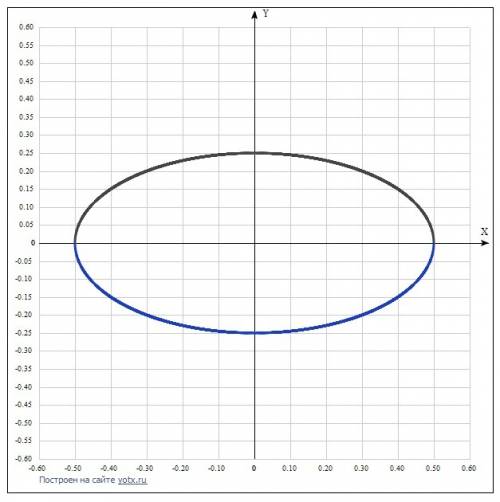
- 1) круг в плоскости под углом 30° к координатной плоскости ХОУ.
Тогда его диаметр в плоскости YOZ виден с размером 0,5*sin 30° = 0.25 см. Полученный эллипс строится по координатам точек по формуле: у = +-(√(0,25 - 4х²))/2.
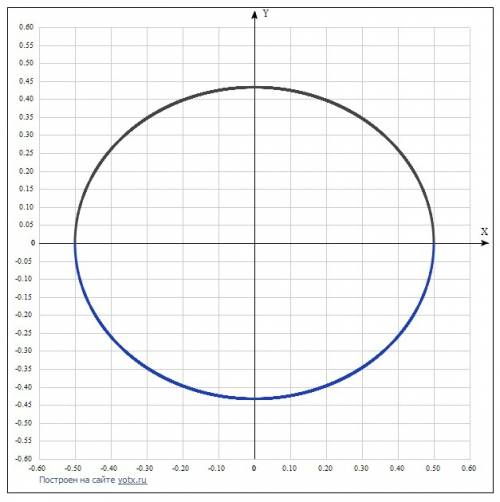
- 2) круг в плоскости под углом 30° к координатной плоскости YOZ.
Тогда его диаметр в плоскости YOZ виден с размером 0,5*sin (90-30)° = 0.433013 см. Полученный эллипс строится по координатам точек по формуле: у = +-(√(0,75 - 3х²))/2.
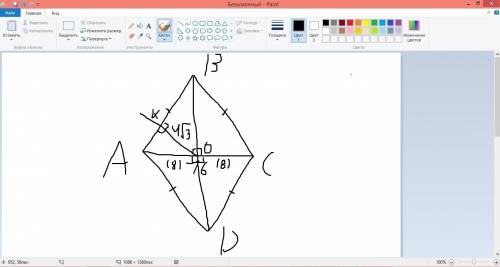
Ну,смотри, AO=OC по свойству п-грамма,а диагонали ромба взаимноперпендикулярнытоже по свойству самого ромба)),тогда можно применить формулу пропорциональных отрезков в прямоугольном треугольнике: OK^2=AO^2-AK^2(48=64-x),где x = 16.Так же по другой формуле можно найти KB: OK^2=AK*KB(48=16x),где x = 3,значит сторона ромба равна 19.Так же для этого треугольника можно применить теорему пифагора: AB^2(16+3=19)=AO^2+x^2(361=64+x),где x равен 297,а значит половина этой диагонали равно корень из 297 = 3 корень из 33,тогда вся диагональ равна 3 корень из 3 *2 = 6 корень из 33
а)
ДС параллельно СД
ДД1 -высота на пл. α =а/2
СС1 -высота на пл. α =ДД1=а/2
б)
линейный угол двугранного угла DABM -это угол между плоскостями которым принадлежат прямые ДА и ВМ (см. рис)
в)
ДД2 -высота на АВ
ДД2=ДА*sin60=a√3/2
sinДД2Д1=ДД1/ДД2=(а/2)/(a√3/2)=1/√3