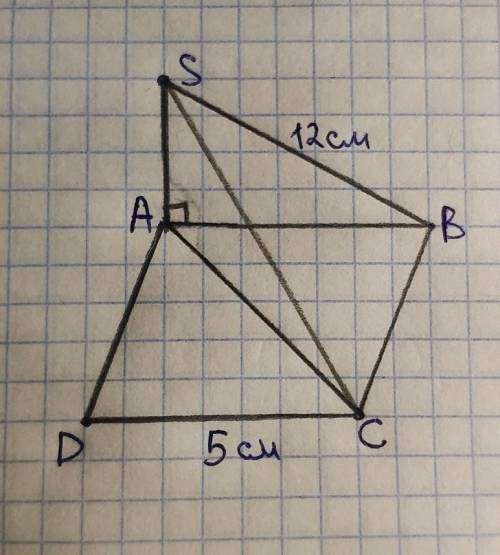
Все стороны квадрата равны. АВСD – квадрат по условию, тогда AD=AB=CD=5 см.
Углы квадрата прямые, то есть угол ADC=90°, следовательно ∆ADC – прямоугольный.
В прямоугольном треугольнике ASC по теореме Пифагора:
AC²=AD²+CD²
AC²=5²+5²
АС²=25+25
АС=√50 см
Если прямая перпендикулярна плоскости, значит она перпендикулярна всем прямым, лежащим на этой плоскости. Исходя из этого: так как SA перпендикулярна АВСD, то угол SAB=угол SAC=90°.
Так как угол SAB=90°, то ∆SAB – прямоугольный.
В прямоугольном треугольнике SAB по теореме Пифагора:
SB²=SA²+AB²
12²=SA²+5²
144=SA²+25
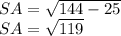
Так как угол SAC=90°, то ∆SAC – прямоугольный.
В прямоугольном треугольнике SAC по теореме Пифагора:
SC²=SA²+AC²
SC²=(√119)²+(√50)²
SC²=119+50
SC²=√169
SC=13 см.
ответ: 13 см.
Объяснение:
Во второй части рассказа важную роль для раскрытия образа коллежского асессора играют метафора («окаменел»), сравнение («казалось… от лица и глаз его посыпались искры»), олицетворение (коробки, узлы «съежились Так в рассказе «Толстый и тонкий» Чехов высмеивает низкопоклонство, трусость, при героя. Причем делает Тонкий это неосознанно, по привычке, не обращая внимания на слова бывшего товарища: «Ну, полно… И к чему этот тон?». Нравственное значение произведения. Невеселые мысли вызывает у читателя содержание рассказа и его анализ. «Толстый и тонкий» - это пример того, до какого самоуничижения может дойти человек в стремлении выслужиться, угодить
1) см. рис
А и А1 точки пересечения окружностей с центрами О и К
АР перпендикуляр на продолжение ОК
АР=у
ОР=х
ОА=4
КА=8
ОК=6
х²+у²=4²=16
(х+6)²+у²=8²=64 ⇒ у²=64-(х+6)², подставляем в первое
х²+64-(х+6)²=16
х²+64-х²-12х-36-16=0
12х=12
х=1
у=√(16-1)=√15
l -расстояние от т.О до ц. окр. М касающихся одновременно двух данных, т.е. в т.А и А1 (необходимо найти МА)
МА²=(х+l)²+у²=(1+l)²+15
2)
АВС - треугольник, а=60, В=50, С=70, т.Н пересечение
АА1, ВВ1, СС1 высоты.
<АНС1=<СНА1=<3 (вертикальные)
<BHC1=<CHB1=<1 (вертикальные)
<BHA1=<AHC1=<2 (вертикальные)
ΔВНА1 подобен ΔВСВ1 ⇒<BHA1=<С=70
ΔВНС1 подобен ΔВАВ1 ⇒<BHC1=<А=60
ΔСНА1 полобен ΔСВС1 ⇒<СНА1=<В=50
3) см рис. 2
<α=180-90-48=42°