20°
Объяснение:
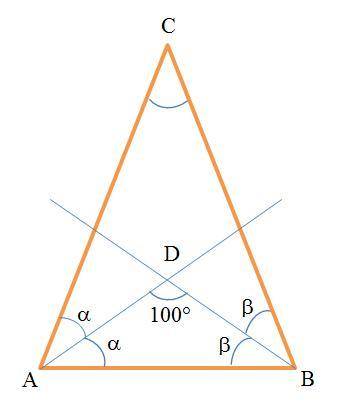
Дано (см. рисунок):
ΔАВС - равнобедренный
AD - биссектриса угла А
BD - биссектриса угла В
∠ADB = 100°
Найти: ∠С
Решение.
Так как треугольник ABC равнобедренный, то у него углы при основании равны ∠А=∠В. Биссектриса делит угол пополам, поэтому α=∠А/2 и β=∠В/2. Но ∠А=∠В и поэтому α=β. Значит, треугольник ADB также равнобедренный.
Найдём углы α и β. Сумма внутренних углов треугольника равна 180°: α + β + 100° = 180°. В силу этого α = β = (180-100)/2 = 40°.
Тогда ∠CАВ=∠СВА=2·α=2·40°=80°. Опять используем свойство:
Сумма внутренних углов треугольника равна 180°.
В силу этого ∠CАВ+∠СВА+∠С=180°. Отсюда
∠C=180°-(∠CАВ+∠СВА)=180°-(80°+80°)=180°-160°=20°.
ответ: 20°
Построим высоту СН к стороне АВ
В прямоугольном треугольнике СВН угол В=45 градусов (по условию), тогда угол ВСН=90-45=45 градусов, следовательно, треугольник равнобедренный, значит, ВН = СН
Известно что ВС=6, пусть АН=ВН=х, тогда по теореме Пифагора ВС^2=ВН^2+СН^2
Уравнение:
36=х^2 + x^2
36=2x^2
x^2=18
х=корень из 18;
Треугольник АНС - прямоугольный
Угол А=60 градусов (по условию), тогда угол НСА=90-60=30 градусов
Пусть АС=2х, тогда АН=х (так как катет, лежащий против угла, равного 30 градусов, равен 1/2 гипотенузы)
По теореме Пифагора АС^2=АН^2+НС^2
Уравнение:
4х^2=18+х^2
4х^2 - х^2 = 18
3х^2 = 18
х^2 = 6
х = корень из 6;
Тогда Ас = 2х = 2 корня из 6
ответ: 2 корня из 6
Удачи ;)
r вписанной окружности равен √3a/2 т.е.
r=√3*6√3/2=9см
Длина окружности высчисляется по формуле p=2πr, т.е.
p=18π
Площадь находим по формуле S=πr^2 т.е.
S=81π
ответ: p=18π, S=81π