Так как в △ABC стороны AC и BC равны, то этот треугольник равнобедренный, тогда сторона AB является основанием равнобедренного треугольника, а ∠A и ∠B — углы при основании равнобедренного треугольника. Тогда:
∠A = ∠B.
Так как ∠A и ∠B равны, то синусы этих углов будут также равны.
В △AHB ∠AHB = 90° (так как AH — высота), тогда сторона AB, лежащая напротив прямого угла, является гипотенузой △AHB, а стороны AH и BH —катетами.
В прямоугольном треугольнике синусом острого угла называется отношение катета, который лежит напротив этого угла, к гипотенузе. Напротив ∠B лежит катет AH, тогда:
sin∠B = AH / AB.
По условию AH = 3, а AB = 10, тогда:
sin∠B = 3/10 = 0, 3.
Так как синус ∠B равен синусу ∠A (он же ∠BAC), то:
sin∠A = 0, 3.
ответ: sin∠A = 0, 3.
1.
Расстояние между точкой A & прямой a — проекция наклонной Ba, или просто — катет.
Другого определения здесь невозможно дать, этот треугольник обязательно должен быть прямоугольным.
<B = 30°; Теоерема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Напротив угла <B — лежит катет Aa, тоесть: Aa = Ba/2.
Катет Aa — мы можем найти только теоремой Пифагора:
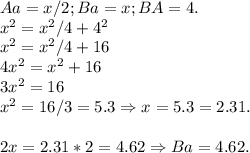
Вывод: Aa = 2.31.
2.
<A = 90°; <B == <C => BA == AC.
BC (гипотенуза) = 14; по теореме Пифагора:
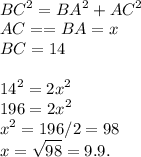
Нарисуем дополнительную высоту, проведённую через прямой угол: Высота AM.
В равнобедренном прямоугольном треугольнике — высота, проведённая к гипотенузе — это — и медиана, и высота, и биссектриса.
То есть: AM == MC = 14/2 (свойство медианы в прямоугольном треугольнике) = 7.
Вывод: AM = 7.
3.
<B = 30° => AC = BC/2 (теорема о 30-градусном угле).
Опять же, теорема Пифагора:
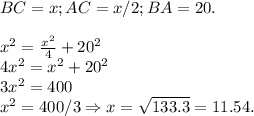
Высоту нарисуем дополнительную, в рисунке — её нет.
Добавим новую точку на гипотенузе BC — пусть будет — M.
Отрезок AM — это и есть расстояние между прямой a — и точкой A.
<MAC = 90 - <C = 90-60 = 30° => MC = AC/2 (теорема о 30-градусном угле).
MC = AC/2 => MC = 11.54/2 = 5.8.
По теореме Пифагора:
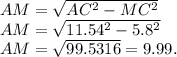
Вывод: MC = 9.99.
\\ВНИМАНИЕ!
Теорема Пифагора такова: Сумма квадратов катетов равна квадрату гипотенузы, тоесть: 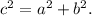 \\
\\
У таких задач есть типовой прием решения.
Пусть х = AD/AC;
Надо провести через точку D прямую II BC до пересечения с АМ в точке N. Ясно, что
AN/AM = x;
Есть два соотношения (первое следует из подобия тр-ков NDK и BKM, а второе - из подобия треугольников AND и AMC)
ND/BM = KN/KM и ND/MC = AN/AM;
M - середина ВС, то есть ВМ = МС, и
KN/KM = AN/AM = x;
При этом KM = АМ/2; KN = АК - AN = AM/2 - AM*x; KN/KM = 1 - 2*x;
то есть 1 - 2*х = х; :)
x = 1/3;
То есть AD = AC/3, а DC = 2*AC/3, и AD/DC = 1/2;