Поскольку плоскость сечения параллельна оси цилиндра, сечением будет прямоугольник с высотой H, равной высоте цилиндра, и основанием длиной L, являющемся хордой, лежащей в основании цилиндра. Также известно, что диагональ прямоугольника имеет наклон в 60 градусов к его основанию. Отсюда можно записать следующие соотношения:
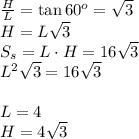
Далее проведем отрезки, соединяющие концы хорды с центром основания цилиндра. Получится равнобедренный треугольник с углом в вершине 120 градусов и бедрами, равными радиусу основания цилиндра. Проведя в этом треугольнике высоту из вешины к хорде, получим два прямоугольных треугольника, одним из катетов которых является половина хорды. Поскольку угол между этими катетами и гипотенузой равен 30 градусам, можно записать следующее соотношение между длиной хорды и радиусом основания цилиндра:
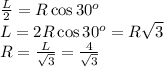
Запишем теперь выражение для площади боковой поверхности цилиндра:
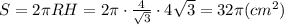
ответ: Площадь боковой поверхности цилиндра равна 32пи кв. см
15:9:6= 5:3:2
И во втором треугольнике АСД стороны АС=15, СД=10 и АД=25
25:15:10=5:3:2
Значит эти треугольники подобны. Отметить равные углы. Проти маленьких сторон Угол ВАС в треугольнике АВС и угол САД против стороны СД в треугольнике САД. Эти углы внутренние накрест лежащие при папаллельных прямых ВС и АД секущей АС.
Трапеция, Две стороны ав и сд параллельны.