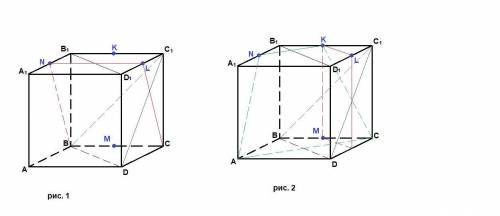
Дано:
АС=7 см;
АВ=25 см;
ВС=24 см.
СО – высота, проведенная к АВ.
Высота, пересекаясь со стороной, к которой проведена, образует прямой угол.
То есть угол ВОС=90° и угол АОС=90°.
Следовательно ∆ВОС – прямоугольный с прямым углом ВОС и ∆АОС – прямоугольный с прямым углом АОС.
Пусть АО=х, тогда ВО=АВ–АО=25–х.
По теореме Пифагора в прямоугольном треугольнике ВОС:
ВС²=ВО²+СО²
СО²=ВС²–ВО²
СО²=24²–(25–х)²
СО²=576–625+50х–х²)
СО²=–х²+50х–49 (Ур 2)
По теореме Пифагора в прямоугольном треугольнике АОС:
АС²=АО²+СО²
СО²=АС²–АО²
СО²=7²–х²
СО²=49–х² (Ур 2)
Тогда можем составить уравнение, объединив Ур 1 и Ур 2, получим:
–х²+50х–49=49–х²
50х=98
х=1,96
Тоесть АО=1,96 см.
Подставим значение АО и известное значение АС в уравнение СО²=АС²–АО², получим:
СО²=49–3,8416
СО²=45,1584
СО=6,72 см.
ответ: 6,72 см.
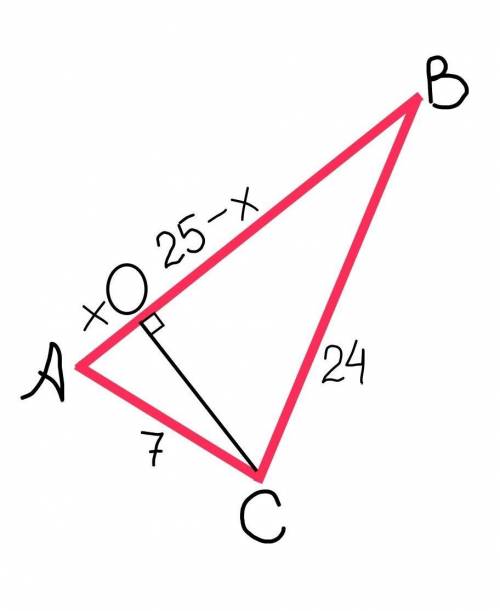
a) АА₁║(ВСС₁)
b) AA₁║(BDD₁)
c) AA₁ ∩ (BDC₁)
d) AA₁║(KLM)
e) AA₁ ∩ (CNK)
f) AA₁ ∩ (LMN)
Объяснение:
Если прямая, не лежащая в плоскости, параллельна прямой, лежащей в плоскости, то она параллельна плоскости.
а) АА₁║ВВ₁, ВВ₁║СС₁ как противоположные стороны квадрата,
значит АА₁║СС₁.
СС₁ ⊂ (ВСС₁), ⇒ АА₁║(ВСС₁).
b) АА₁║ВВ₁, ВВ₁ ⊂ (BDD₁), ⇒ AA₁║(BDD₁) (рис. 1)
c) Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
АА₁║ВВ₁, ВВ₁ ∩ (BDC₁), ⇒ AA₁ ∩ (BDC₁) (рис. 1)
d) Точки К и М - середины равных параллельных ребер В₁С₁ и ВС, значит В₁К║ВМ и В₁К = ВМ, ∠В₁ВК = 90°, значит ВВ₁КМ - прямоугольник, тогда ВВ₁║КМ.
АА₁║ВВ₁, ВВ₁║КМ, ⇒ АА₁║КМ,
КМ ⊂ (KLM), ⇒ AA₁║(KLM) (рис. 2)
e) Параллельные плоскости пересекаются третьей плоскостью по параллельным прямым.
AA₁ ∩ (CNK) (рис. 2)
f) ВВ₁ ∩ (LMN), AA₁║BB₁, ⇒ AA₁ ∩ (LMN)(рис. 1)