Дано:
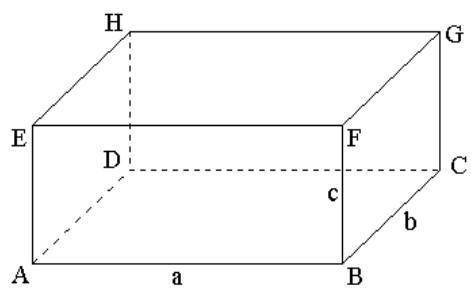
ABCDEFGH - прямоугольный параллелепипед
AB:BC:BF = 1:2:3
Sполн = 550 см²
------------------------------------------------------------------------------
Найти:
AB - ?, BC - ?, BF - ?
Пусть AB = x см, тогда BC = 2x см, и BF = 3x см.
Запишем формулу площади полной поверхности параллелепипеда:
Sполн = 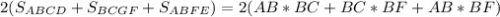
Именно по такой формуле площади полной поверхности параллелепипеда мы найдем все длины параллелепипеда:
Sполн = 2(AB×BC+BC×BF+AB×BF)
550 = 2(x × 2x + 2x × 3x + x × 3x см)
550 = 2(2x² + 6x² + 3x²)
550 = 2×11x²
550 = 22x²
x² = 25
x = √25
x = 5 см ⇒ AB = 5 см, следовательно:
BC = 2x = 2×5 см = 10 см
BF = 3x = 3×5 см = 15 см
ответ: AB = 5 см, BC = 10 см, BF = 15 см
P.S. Рисунок показан внизу↓
Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство. Пусть в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).
Рис.1
Докажем, что ∠ С > ∠ В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD < АВ, то точка D лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, ∠ C > ∠ 1. Угол 2 — внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2 равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠ С > ∠ 1, ∠ 1 = ∠ 2, ∠ 2 > ∠ B. Отсюда следует, что ∠ С > ∠ В.
Справедлива и обратная теорема (ее доказательство проводится методом от противного).
Теорема 2. В треугольнике против большего угла лежит большая сторона.
Из теоремы 1 вытекает
Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Доказательство следствия проводится методом от противного.
Из следствия 1 следует, что если три угла треугольника равны, то треугольник равносторонний.
Из теоремы 2 получаем
Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.
С использованием теоремы 2 устанавливается следующая теорема.
Теорема 3. Каждая сторона треугольника меньше суммы двух других сторон.
Следствие 4. Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства:
АВ < АС + СВ, АС < АВ + ВС, ВС < ВА + АС.