если их можно совместить и при наложении они совпадают.
Если при наложении они совпадают. Равные отрезки имеют одинаковые длины.
Если при наложении они совпадают. т.е. вершины совпадут. а лучи, выходящие из вершин, тоже при наложении совпадают. Равные углы имеют равные градусные меры.
Треугольники называют равными, если при наложении друг на друга они совпадают. У равных треугольников все три стороны одного равны трем сторонам другого. То же можно сказать и об углах.
2 представьте, построили два равных прямоугольных треугольника, у которых катеты по 3 см 4 см, а гипотенузы по 5 см. у меня нет возможности попасть в приложение. поэтому не могу Вам кинуть рисунок. Но это не сложно. АВ=ТР= 3 см, ВС= РК=4см, АС=ТК=5 см, и тогда треугольники АВС и ТРК равны.
3.
1.FDE
2.KNM
3.SKT
DBC
5. MKC
Нарисуем этот треугольник.
Обозначим точки буквами- см.рисунок.
Получились прямоугольные треугольники, высоты в который определяются по формуле высоты равностороннего треугольника
h=(а√3):2
Найдем сторону ВК в треугольнике КВМ
3=(ВК√3):2
(ВК√3)=3*2=6
ВК=6:√3=2√3
По той же формуле найдем АВ
5=(АВ√3):2
АВ√3=5*2=10
АВ=10:√3=(10√3):3
АК=(10√3):3 -2√3=(10√3 -6√3):3=(4√3):3
КН=√3(4√3):3):2=12:6=2см
рисунок - во вложении
----------------------------------------------
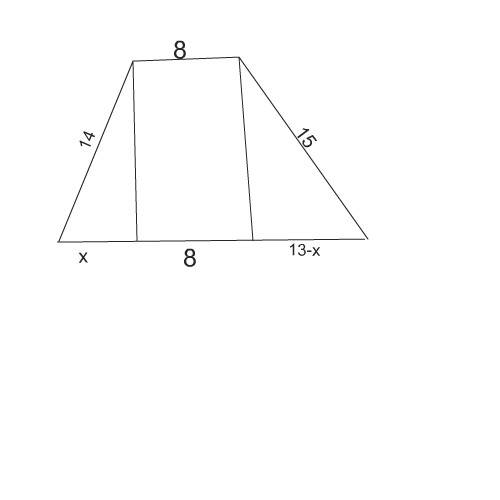
Рисуем трапецию.
Опустим из ее углов при меньшем основании высоты на нижнее основание.
Получили один прямоугольник и два прямоугольных треугольника при боковых сторонах как гипотенузах.
Найдем значение высот и приравняем их.
Для этого отрезок основания при боковой стороне 14 обозначим х, а отреок ( катет) при боковой стороне 15 будет 21-х-8=13-х
14²-х²=15²-(13-х)²
Из этого уравнения найти х, затем из прямоугоьного треугольника с гипотенузой 14 и катетом, равным найденному х, вычислить высоту трапеции.
надеюсь, на фотке решение возможно разобрать)