ответ: На 4 треугольника.
Объяснение:
Соединив одну вершину выпуклого шестиугольники с остальными, мы проводим диагонали. Из одной вершины многоугольника можно повести n-3 отрезка ( диагоналей), где n - количество сторон ( вершин). т.к. выбранная вершина уже соединена с соседними сторонами многоугольника, и ее саму нельзя соединить с самой собой).
Следовательно, можно провести 6-3=3 отрезка, которые разделят выпуклый шестиугольник ( неважно, правильный или произвольный) на 4 треугольника. (см. рисунок)
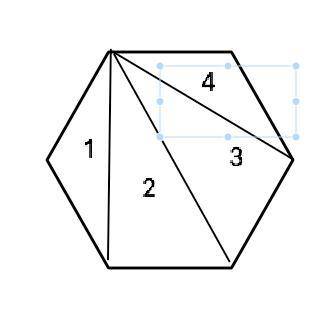
я все на рисунке отмечу
на нем:
1 и 7; 2 и 8 - внешние накрест лежащие углы
3 и 5; 4 и 6 - внутренние накрест лежащие углы
1 и 5; 4 и 8: 2 и 6; 3 и 7 - соответственные углы
3 и 6; 4 и 5 - внутреннние односторонние углы
1 и 8: 2 и 7 - внешние односторонние углы