Обозначим хорду АВ. Расстояние от точки до прямой измеряется длиной проведенного к ней перпендикуляра.⇒ перпендикуляр ВЕ=6 см.
Из ∆ АМВ по т.Пифагора катет ВМ=8.
ВК - отрезок секущей и является хордой.
ВК||АЕ по условию.
Проведем диаметр АС.
Диаметр перпендикулярен касательной, следовательно, перпендикулярен и параллельной ей секущей.
АС⊥ВК. Диаметр, перпендикулярный хорде, делит ее пополам. КМ=ВМ.=8.
Диаметр - наибольшая хорда окружности.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.
АМ•СМ=КМ•МВ
6•СМ=64⇒ СМ=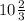 3 см ⇒
3 см ⇒
Диаметр АС=АМ+МС=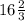 см⇒
см⇒
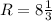 см
см
№49: DK = 2
№50: MD = 16
Объяснение:
№49:
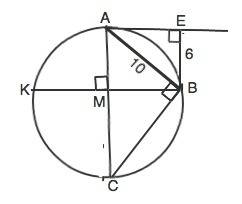
Т.к. ABCD - параллелограмм, AB || CD, то есть AB || CK. Тогда BK - секущая при параллельных прямых. Следовательно, ∠ABK=∠BKC, как накрест лежащие углы при параллельных прямых. Рассмотрим треугольник BCK: ∠CBK=∠BKC (∠ABK=∠CBK, по условию, а ∠ABK=∠BKC), следовательно, треугольник BCK равнобедренный. По свойству равнобедренного треугольника боковые стороны равны, то есть BC = CK = 8 (по условию). BC = CD + DK, CD = AB = 6 (по свойству параллелограмма), тогда DK = BC - CD = 8 - 6 = 2.
№50:
Т.к. ABCD - параллелограмм, BC || AD, то есть BC || MD. Тогда CM - секущая при параллельных прямых. Следовательно ∠BCM=∠CMA, как накрест лежащие углы при параллельных прямых.. Рассмотрим треугольник CAM: ∠CMA=∠MCA (∠MCA = ∠BCM по условию, а ∠BCM=∠CMD), следовательно, треугольник CAM равнобедренный. По свойству равнобедренного треугольника боковые стороны равны, то есть AM = AC = 10 (по условию). MD = AM + AD, BC = AD = 6 (по свойству параллелограмма), тогда MD = AM + AD = 10 + 6 = 16.
1 ) составить уравнение
х+3х+х+3х=180
8х=180
х=22,5 см
22,5*3=67,5 см
ответ;22 , 5...67,5...22,5...67,5...