рассм. тр-к АДС уг.СДА=90 гр, уг. САД=60 гр., следовательно угол
ДСА=90-60=30 гр. треугольник прямоугольный, катет лежащий против угла 30 равен 1/2 гипотенузы, АД=(1/2)*АС=10/2=5 см, далее рассмотрим прямоугольный треугольник АДЕ, в котором уг.ДАЕ=30 гр, следовательно, ДЕ=(1/2)*АД=5/2=2,5 см
Построение сводится к проведению перпендикуляра из точки к прямой.
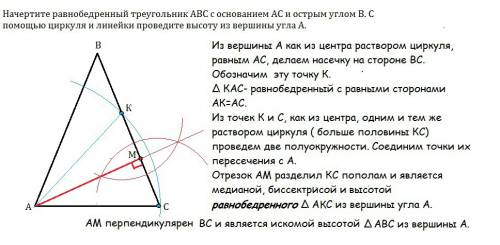
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Треуг. АСД - прямоугольный, СД=АСsinA=10*0.5=5 (см), угол АСД=60град;
Треуг. СДЕ - прямоугольный, угол ДСЕ=90-60=30 град, СЕ=СДcosДСЕ=5*√3/2;
Треуг. АСЕ - прямоугольный, по теореме Пифагора
АЕ=√(АС2+СЕ2)=√(100+25*3/4)=√(475/4)=2,5√19