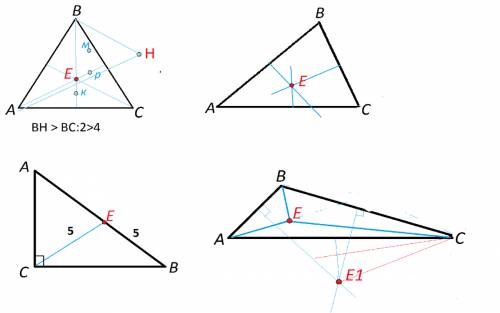
ищем уравнение пряммой ВС
пряммая проходящая через точки  имеет вид
имеет вид
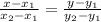
ищем уравнение высоты АД
поэтому уравнение стороны ВС имеет вид
для угловых коэффициентов перпендикулярных пряммых выполянется соотношение 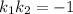 , поэтому угловой коэффициент прямой, содержащей высоту АД равен
, поэтому угловой коэффициент прямой, содержащей высоту АД равен
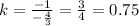
пряммой, содержащей высоту АД, принадлежит точка А, поэтому
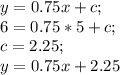
ищем координаты точки Д, как точки пересечения пряммых ВС и АД
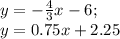
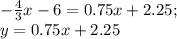
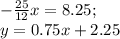
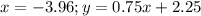
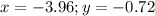
ищем длину высоты АД по формуле расстояния между двумя точками
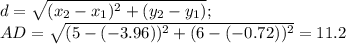
ищем координаты точки М как середины отрезка ВС
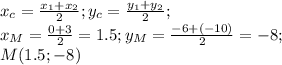
ищем уравнение медианы АМ
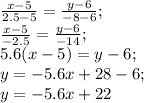
ищем длину стороны АС
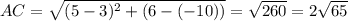
ищем длину стороны ВС
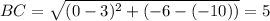
ищем длину стороны АВ
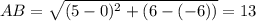
ищем косинус угла В по теореме косинусов
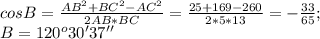
если разрезать данный треугольник пополам - по высоте, то получатся два прямоугольных треугольника, в которых
a=катет1= высота =6
b=катет2= половина основания =(х+6)/2
c=гипотенуза =боковая сторона = х
по теореме Пифагора
c^2 = a^2 +b^2
x^2 = 6^2 +((х+6)/2)^2
x^2 = 36 +(х+6)^2/4 - домножим обе части на 4
4x^2 = 144 +(х+6)^2
4x^2 = 144 +х^2+24x+36
4x^2 -х^2-24x-180=0
3x^2 -24x-180=0 - делим на 3
x^2 -8x-60=0
квадратное уравнение
D= 304
x1=4-2√19 < 0 - по смыслу не подходит
x2=4+2√19 - боковая сторона
6+x2 =6+4+2√19=10+2√19 или 2(5+√19) - основание