В основании правильной пирамиды - правильный треугольник. Вершина S проецируется в центр О основания. Высота правильного треугольника СН= (√3/2)*а, где а - сторона треугольника. СН=13√3/2. В правильном треугольнике высота=медиана и делится центром в отношении 2:1, считая от вершины. => HO=(1/3)*CH, а СО=(2/3)*СН или СО=13√3/3, НО=13√3/6.
По Пифагору:
Боковое ребро пирамиды SC=√(CO²+SO²) = √(313/3).
Апофема (высота боковой грани) SH=√(НO²+SO²) = √(745/12).
Боковая поверхность Sбок = (1/2)*3*АВ*SH =(39/4)*(√(745/3).
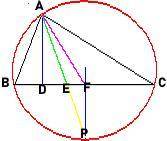
Допустим возьмём треугольник ABC. Проведём высоту, биссектрису и медиану из вершины A. Поставим 3 точки: D E и F, где D это основание высоты, E основание биссектрисы и F основание медианы.
Также нарисуем описанную окружность этого треугольника. Пусть P — точка пересечения прямой AE с этой окружностью. Тогда P — середина дуги BC. Поэтому прямая, проведённая через точку P параллельно AD, перпендикулярна хорде BC (т.к. AD⊥AC) и, поэтому проходит через её середину, т.е. точку F.
Доказав, что E лежит между D и F мы докажем что в любом неравнобедренном треугольнике биссектриса проходит между высотой и медианой проведенными из той же вершины.
Прямая AD параллельна FP. Биссектриса-это AE, но мы её продлим до AP. Точка E находится на отрезке AP И любая точка находящаяся на AP (кроме самих точек A и P) будет между параллельных линий AD и FP. Значит точка E находится между параллелей AD и FP. Также точка E находится на отрезке DF, ведь точки D и F на параллелях AD и FP.