См. рис. во вложении
Для построения будем использовать свойста подобия треугольников.
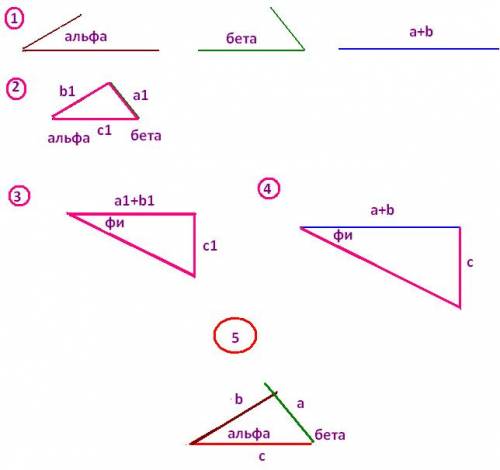
1. Дано: два угла и отрезок.
2. Строим вс треугольник с углами альфа и бета и произвольными сторонами а1 , в1 и с1
3. К отрезку а1+в1 к крайней точке восстанавливаем перпендикуляр длиной с1. Проводим к его концу прямую и получаем угол фи.
4. К отрезку а+в проводим в левой крайней точке луч под углом фи, а справа перпендикуляр. Пересекаясь с перпендикуляром прямая отсечет на ней отрезок с, т.к. треугольники будут также подобны.
5 По двум углам и полученной строне с строим искомый треугольник. Проверяем совпала ли сумма а+в полученных с заданными. Должна совпасть, если все сделали правильно.
(2*mc)^2 = 2*(a^2 + b^2) - c^2;
(2*mb)^2 = 2*(a^2 + c^2) - b^2;
(2*ma)^2 = 2*(b^2 + c^2) - a^2;
4*(ma^2 + mb^2 + mc^2) = 2*a^2 + 2*b^2 - c^2 + 2*a^2 + 2*c^2 - b^2 + 2*b^2 + 2*c^2 - a^2 = 3*(b^2 + c^2 + a^2); это всё
формулу для длины медианы (2*mc)^2 = 2*(a^2 + b^2) - c^2; лучше всего запоминать именно в такой форме. Получается она элементарно - если продолжить медиану mc на "свою длину" за точку пересечения со стороной c, то треугольник "достраивается" до параллелограмма, в нем диагонали равны с и 2*mc, а стороны a и b. Если теперь записать теорему косинусов для двух треугольников - исходного с^2 = a^2 + b^2 - 2*a*b*cos(Ф); и треугольника со сторонами a, b и 2*mс
(2*mс)^2 = a^2 + b^2 + 2*a*b*cos(Ф); и сложить, как раз и получится нужная формула.