ответ:Решение.
а) Обозначим буквой E точку пересечения отрезков MK и AB. Углы ∠ALB и ∠LAD равны, как накрест лежащие углы; аналогично ∠CLD = ∠ADL, как накрест лежащие. Отсюда получаем, что ∠BAL = ∠BLA, ∠CDL = ∠CLD, то есть треугольники ABL и CLD равнобедренные (AB = BL, CL = CD). Тогда биссектрисы этих треугольников BM и CK являются также высотами и медианами. Значит, точки M и K являются серединами сторон AL и DL соответственно. Отсюда следует, что отрезок MK является средней линией треугольника ALD. Значит, MK || AD.
Теперь если рассмотреть треугольник ABL, получаем, что отрезок EM параллелен стороне BL и исходит из середины стороны AL. Отсюда следует, что EM является средней линией этого треугольника, а значит точка E — середина стороны AB. Что и требовалось доказать.
б) Рассмотрим 4-угольник MLKN. Из предыдущего пункта получили, что ∠M = 90°, ∠K = 90°, откуда следует, что
То есть у данного 4-угольника суммы противоположных углов дают , откуда следует, что вокруг него можно описать окружность. Соединим точки N и L (пересечение с MK в точке F) — получим 2 прямоугольных треугольника NML и NKL. Тогда центр описанной окружности лежит на середине общей гипотенузы NL.
Теперь заметим, что треугольники MFL и NFK подобны по 2 углам (∠MFL = ∠NFK, как вертикальные; ∠MLF = ∠NKF, как вписанные углы, опирающиеся на одну и ту же дугу MN). Тогда
Аналогично треугольники NMF и KFL подобны по 2 углам (∠NFM = ∠KFL, как вертикальные; ∠MNF = ∠FKL, как вписанные углы, опирающиеся на одну и ту же дугу ML). Тогда
Поделим соотношения друг на друга:
Из подобия треугольников NLC и NFK (по 3-м углам) получим, что Аналогично из подобия треугольников NLB и NFM получим, что , откуда следует:
Окончательно получаем, что
ответ: 5 : 14.
Объяснение:
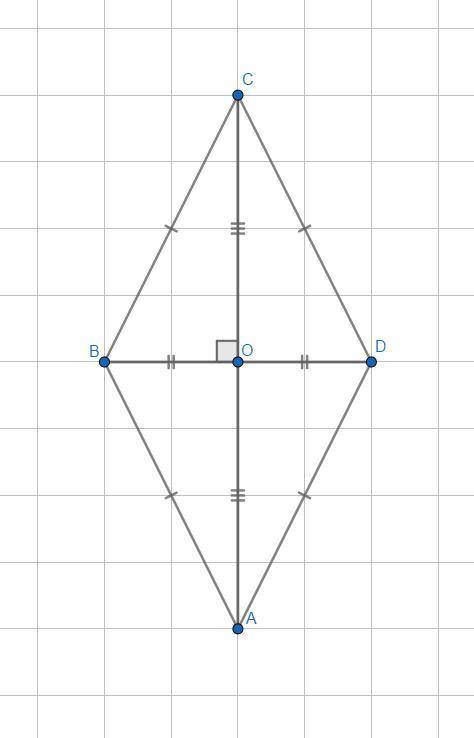
В ромбе диагонали точкой пересечения делятся пополам (АО=ОС и ВО=OD).
Пусть ВО=х, тогда:
AC-BD=14
AC-2x=14
AC=14+2x
2·OC=2(x+7)
OC=x+7
Из ΔBCO по т. Пифагора:
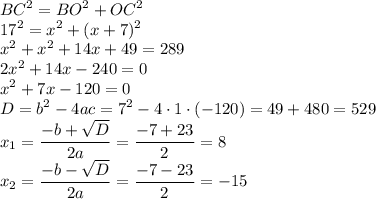
x=-15 не подходит по смыслу задачи, поэтому один корень х=8.
ВО=х=8 см
ОС=х+7=8+7=15 см
АС=АО+ОС=15+15=30 см
BD=BO+OD=8+8=16 см
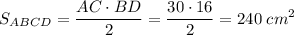
Вспомним такую формулу: 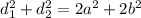 , где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).
, где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).
Найдем диагонали, составив систему:
Пусть АС=х, BD=y.
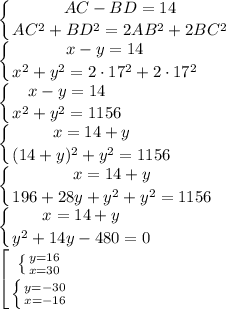
Отрицательные значения нам не подходят, так как длинна - величина неотрицательная.
Тогда AC=x=30см, BD=y=16см.
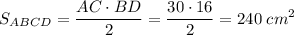
ответ: 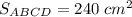
СН перпенд-но АД ---> ДН=(25-7)/2=9, АН=(25+7)/2=16
СН - высота, проведённая из вршины прямого угла ΔАСД.
--->CH²=AH*ДН=16*9=144 , СН=12
S=(25+7)/2 *12=192