(см. объяснение)
Объяснение:
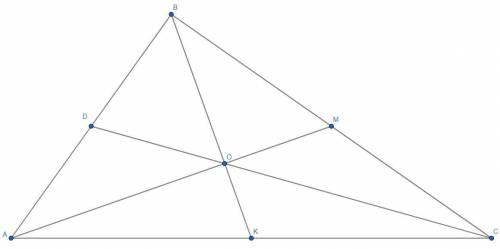
Т.к. все медианы треугольника пересекаются в одной точке, то CD проходит через точку O. Медианы точкой пересечения делятся 2:1, считая от вершины. Тогда BO=8 и AO=6. Т.к. медианы AM и BK пересекаются под прямым углом, то треугольник AOB прямоугольный, тогда его медиана OD равна половине гипотенузы, которую можно найти по теореме Пифагора, как AB²=BO²+AO² => AB=10. Тогда OD=5. Применив еще раз свойство деления медиан точкой пересечения, получим, что CD=15.
Задача решена!
У них коэффициент при прямой
Значит они направлены по одну сторону относительно к друг другу .
То есть биссектриса направлена , к стороне
То есть биссектриса имеет начало и конец в очках
Точка пересечения
То есть часть отрезка на которые поделила биссектриса равна
Длина стороны
Координаты третьей стороны
По теореме о биссектрисе
Решая получим что уравнение стороны