 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 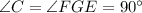 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 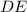 , то
, то 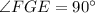 ).
).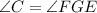 и
и 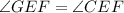 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: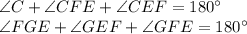
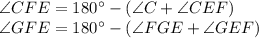
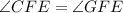 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: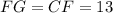
 . Смотрите второй рисунок.
. Смотрите второй рисунок.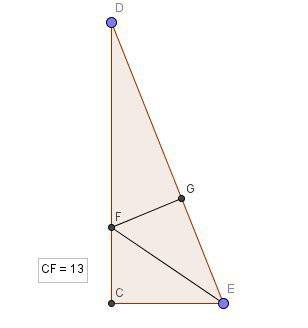
Объяснение:
1) Рассмотрим ΔАСО и ΔFDO.
∠CAO=∠ DFO - по условию,
AO=FO - по условию,
∠СОА = ∠DOF - как вертикальные.
⇒ΔАСО = ΔFDO по стороне и двум прилежащим к ней углам ( ІІ признак равенства треугольников)
Из Равенства треугольников следует равенство сторон: СО=DO
2) Рассмотрим ΔCBO и ΔDEO.
CB=DE и BO=EO - по условию, СО=DO - по доказанному выше.
⇒ΔCBO = ΔDEO по трём сторонам (ІІІ признак равенства треугольников)
Из равенства треугольников следует равенство углов: ∠CВO=∠DЕO,
что и требовалось доказать.
SinA=0.6=6/10=3/5
Синус острого угла прямоугольного треугольника – отношение противолежащего катета к гипотенузе. Sin A=BC/AB
Значит BC=3 ед., AB=5 ед .
Построение:
- построим первый луч и отложим на нём 3 равных отрезка произвольной длины.
- построим второй луч и отложим на нём 5 отрезков такой же длины.
- построим прямой угол С.
- с центром в точке С проведём окружность радиусом равным длине 3-х отрезков. Получим точку B.
- с центром в точке В проведём окружность радиусом равным длине 5-ти отрезков. Получим точку А.
- соединим точки А и В.