Треугольник равнобедренный, значит боковые стороны равны.
1 случай:
Пусть х(см)-длина боковой стороны, тогда (х-4)см - длина основания, по условию периметр равен 15см. Составим и решим уравнение:
х+х+(х-4)=15;
х+х+х-4=15;
3х=19,
х=19:3
х=6 1/3
6 1/3(см)-длина одной боковой стороны
6 1/3 +6 1/3=12 2/3(см)- сумма боковых сторон.
2 случай:
Пусть х(см)-длина основания, тогда длина боковой стороны (х-4)см. Составим и решим уравнение:
х+(х-4)+(х-4)=15;
х+х-4+х-4=15;
3х=23,
х=7 2/3
7 2/3(см)-длина основания
7 2/3-4=3 2/3(см)-длина боковой стороны
3 2/3+3 2/3=7 1/3(см)-сумма боковых сторон (не удовлетворяет теореме о неравенстве треугольника)
ответ: 12 2/3(см).
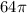 см³.
см³.
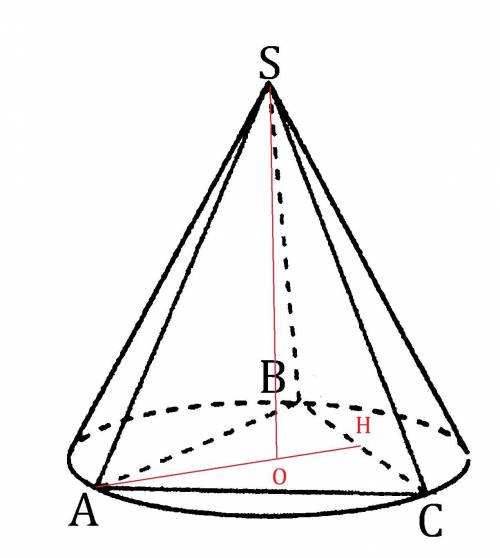
Обозначим данную пирамиду буквами 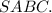
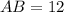 см.
см.
Проведём высоту пирамиды SO.
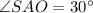
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
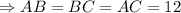 см.
см.
Проведём высоту  в
в 
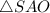 - прямоугольный, так как
- прямоугольный, так как 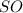 - высота пирамиды.
- высота пирамиды.
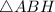 - прямоугольный, так как
- прямоугольный, так как  - высота
- высота  .
.
Так как  - равносторонний ⇒
- равносторонний ⇒  - высота, медиана и биссектриса
- высота, медиана и биссектриса
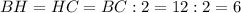 см, так как
см, так как  - медиана.
- медиана.
Найдём  по теореме Пифагора
по теореме Пифагора 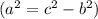 .
.
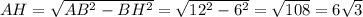 см.
см.
Точка  - пересечение медиан и делит их в отношении
- пересечение медиан и делит их в отношении 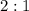 , считая от вершины.
, считая от вершины.
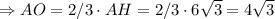 см
см
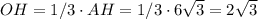 см.
см.
Также 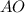 - радиус описанной около
- радиус описанной около  окружности.
окружности.
Рассмотрим 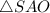
Если угол в прямоугольном треугольнике равен 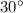 , то напротив лежащий катет равен половине гипотенузы.
, то напротив лежащий катет равен половине гипотенузы.
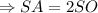
Составим уравнение:
Пусть 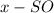 , тогда
, тогда  .
.
И по теореме Пифагора 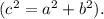
 конуса =
конуса = 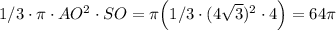 см³.
см³.
Найдите сумму внутренних и сумму внешних углов, взятых по одному при каждой вершине выпуклого пятиугольника.
- - -
Сумма внутренних углов выпуклого многоугольника вычисляется по формуле -
N = 180°*(n - 2)
Где N - сумма внутренних углов выпуклого многоугольника, n - количество сторон (вершин, углов) выпуклого многоугольника.Для пятиугольника -
N = 180°*(5 - 2) = 180°*3 = 540°.
Сумма внешних углов выпуклого многоугольника всегда равна 360°.
Значит, что и у выпуклого пятиугольника сумма внешних углов равна 360°.
Пусть х - боковая сторона треугольника, тогда возможны 2 варианта:
1) Пусть боковая сторона больше основания, тогда основание равно (х-4) и
х+х+(х-4)=15;
3х=19;
х=6,33333
Сумма равна 12.666...
(стороны 6,3; 6,3; 2,3; неравенство треугольников соблюдается)
2) Пусть основание больше боковой стороны, тогда основание равно (х+4) и
х+х+(х+4)=15;
3х=11
х=3,666
Сумма 7,333
(стороны 3,6; 3,6; 7,6; неравенство треугольников не соблюдается, ответ отпадает)
ответ: 12.666...(12 цел. 2/3)