і ми зустрічалися з різними рівняннями і будували їх графіки.
рівнянням фігури на площині в декартових координатах називається рівняння з двома змінними х і у, яке задовольняють координати будь-якої точки фігури, і навпаки: будь-які два числа, які задовольняють це рівняння, є координатами деякої точки цієї фігури.
яке ж рівняння має коло?
для того щоб скласти рівняння кола, згадаємо його властивість, що міститься в означенні кола: усі точки кола розміщені в одній площині з його центром і однаково від нього віддалені.
нехай центр кола м(а; b), а радіус кола r (рис. 140).
позначимо на колі будь-яку точку а (х; у). відстань від точки м до точки а дорівнює r, тобто am = r, але за формулою відстані між двома точками маємо ам2 = (х – а)2 + (y – b)2, або (x – a)2 + (y – b)2 = r2. (1)
координати будь-якої точки цього кола задовольняють рівняння (1). правильно і те, що будь-яка точка, координати якої задовольняють рівняння (1), належить колу.
отже, (x – a)2 + (y – b)2 = r2 — рівняння кола. якщо центр кола (рис. 141) лежить у початку координат, то воно має рівняння х2 + у2 = r2.
розглянемо рівняння (1), у якому х і у — змінні координати точок кола, а числа а і b — відповідно абсциса і ордината центра, r — радіус кола. отже, щоб записати рівняння кола, треба запам'ятати цю формулу і знати координати центра і радіус.
наприклад, нехай m(-1; 2), a r = 2, тоді рівняння кола (x + 1)2 + (y – 2)2 = 4.
виконання вправ
1) які з точок: а(1; 2), в(3; 4), с(-4; 3), d(0; 5), f(5; -1) —лежать на колі, рівняння якого х2 + у2 = 25? 2) запишіть рівняння кола радіуса 1, а координати центра:а) (1; 1);
б) (-1; 1);
в) (1; -1);
г) (-1; -1)
3) укажіть координати центра і радіус кола, яке задане рівнянням:a) (x – 1)2 + y2 = 9;
б) (x + 1)2 + (у + 3)2 = 1;
в) x2 + (y + 1)2 = 2;
г) (x + 1)2 + (y + 2)2 = 7.
4) знайдіть на колі х2 + у2 = 100 точки:а) з абсцисою 6;
б) з ординатою 8.
iv. закріплення й усвідомлення нового матеріалурозв'язування
1. дано точки а(2; 1), в(-2; 5). складіть рівняння кола, діаметром якого є відрізок ав.2. дано точки а(-1; -1) і с(-4; 3). складіть рівняння кола:а) з центром у точці а і яке проходить через точку с;
б) з центром у точці с і яке проходить через точку а.
3. знайдіть на осі ох центр кола, яке проходить через точку а(1; 4) і має радіус 5.4. складіть рівняння кола з центром (1; 2), яке дотикається до осі ох.5. складіть рівняння кола з центром (-3; -4), яке проходить через початок координат.6. доведіть, що відрізок ав, кінці якого а(2; -5) і в(5; -2) є хордою кола (х - 5)2 +(у + 5)2 = 9.7. чи перетинає коло (х + 4)2 + (у – 1)2 = 20 вісь оу? якщо перетинає, то в яких точках?
v. є завдання
вивчити рівняння кола та розв'язати і.
1. коло задане рівнянням (х – 1)2 + (у + 3)2 =10. чи проходить це коло через початок координат? 2. чи перетинає коло (х – 3)2 + (у + 5)2 = 26 вісь ох? якщо перетинає, то знайдіть точки перетину з віссю ох.3. знайдіть рівняння кола, діаметром якого є відрізок ав, якщо а(8; 5), в(2; -3).
vi. підбиття підсумків уроку
завдання класу
1. запишіть рівняння кола.2. знайдіть координати центра і довжини радіусів кіл, зображених на рис. 142. запишіть рівняння цих кіл.
A1.
Sшестиугольника =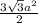 
ответ: 4
A2.
Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:
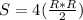
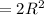
ответ: 1
A3.
Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):
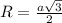
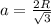
Площадь одного треугольника будет равна:
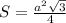
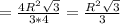
Площадь шестиугольника:
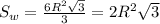
ответ: 2
B1.
Пусть вписанный треугольник - ΔABC, сторона = 
; описанный - ΔA₁B₁C₁, сторона -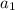 
Для ΔA₁B₁C₁ радиус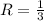 
высоты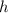 
⇒
⇒ 
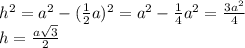
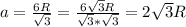
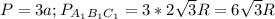
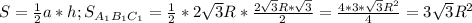
Для ΔABC радиус R =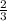 
высоты :
⇒
⇒ 
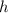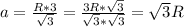
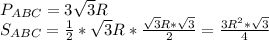
Найдем соотношение периметров и площадей:
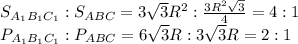
Составляем уравнение
3х+7х+8х=54
18х=54
х=3
СВ=3*8=24