В параллелограмме ABCD биссектрисы углов A и D пересекаются в точке К,которая принадлежит стороне ВС.Найти площадь параллелограмма,если площадь треугольника AKD = 15 см^2.
Объяснение:
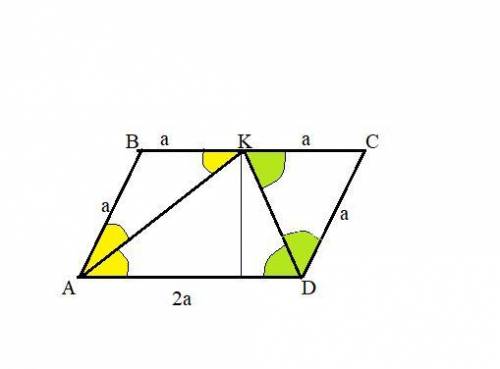
Пусть АВ=DС=а.
По свойству накрест лежащих углов при АD║BC и
-секущей АК ⇒∠DAK=∠AKB ⇒ΔABK равнобедренный и АВ=ВК=а ;
-секущей DК⇒∠АDK=∠СКD ⇒ΔDKС равнобедренный и DС =СК=а.
Значит AD=BC=2a
S(AKD)=0,5*AD*h=0,5*2а*h=a*h
S(ABK)+S(DCK)=0,5*ВК*h+0,5*КС*h=0,5h(BK+KC)=0,5h*2a=a*h ⇒
S(AKD)=S(ABK)+S(DCK)=15 (см²)
S( паралл)=S(AKD)+S(ABK)+S(DCK)=15+15=30 (см²)
36°, 54°, 144°, 126°
Объяснение:
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Пусть 1-й угол четырёхугольника равен 2х, тогда второй угол - 3х, а третий - 8х .
Сумма противоположных углов четырёхугольника (1-го и 3-го) равна
2х + 8х = 10х.
Тогда сумма 2-го и 4-го углов также равна 10х
И 4-й угол равен
10х - 3х = 7х.
Сумма углов четырёхугольника равна 360°.
10х + 10х = 360°
20х = 360°
х = 18°
1-й угол равен 2х = 36°, 2-й угол равен 3х = 54°,
3-й угол равен 9х = 144°, 4-й угол равен 7х = 126°
Рисуй прямоугольник и отмечай точки: А - левый нижний, В - левый верхний, С - правый верхний, Д - правй нижний
РЕШЕНИЕ:
по свойством прямоуг: АВ=ДС=5, ВС=СД=12 , диагонали в прямоуг равны междк собой и точкой пересечения делятся пополам.
РАССМОТРИМ ▲СОД
чтобы найти ▲S = 1/2*h*a ( 1/2 умножить на высоту и сторону, к которой провндена данная высота), В нашем сдучае: 1/2 * ОР*ДС
но у нас нету высоты, тогда проведем высоту из точки О к основанию ДС.
РАССМОТРИМ ▲ОРС, угол Р =90°, ОС =6.5, РС = 2.5
По теореме пифагора:
квадрат гипотинузы равен сумме квадратов катетов прямоугольном ▲ ( сам подставь, мне неудобно писать: ОР, РС - катеты, ДС - гипотенуза) крч в итоге получается : ОР = 6
НАЙДЕМ S :
S = 1/2* 6*5 = 15 cм :)