P = 60 см
Объяснение:
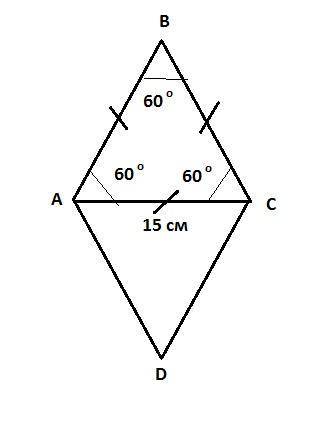
Пусть один из углов ромба равен α, тогда другой угол 2α.
Сумма углов:
α + 2α + α + 2α = 360°
6α = 360°
α = 60°
Значит, Δ ABC - равносторонний.
AB = BC = AC = 15 см
Периметр:
P = 4*15 = 60 см
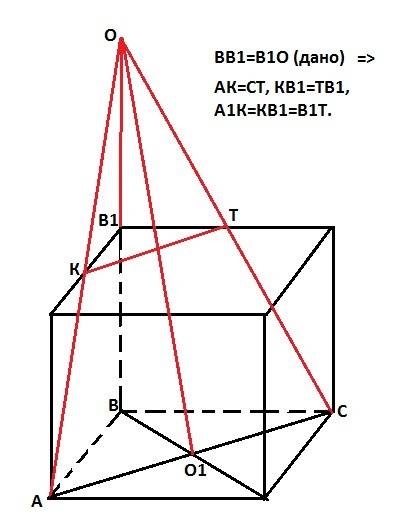
1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано) => АК=ТС => четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.
2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.
1. АВСD - квадрат. Диагонали квадрата взаимно перпендикулярны и точкой пересечения О1 делятся пополам. Следовательно, прямая ОО1 - перпендикулярна АС по теореме о трех перпендикулярах, так как ВО (перпендикулярная АС) - проекция наклонной ОО1. Тогда треугольник АОС - равнобедренный (ОО1 - высота, медиана и биссектриса), АО=ОС и КТ - его средняя линия (так как ВВ1=В1О - дано) => АК=ТС => четырехугольник АКТС - равнобедренная трапеция. Что и требовалось доказать.
2. Средняя линия трапеции - полусумма ее оснований. АС=2√2см (диагональ квадрата со стороной = 2см), а КТ=√2 (по Пифагору, так как треугольник КВ1Т - прямоугольный, равнобедренный, с катетами = 1). Тогда средняя линия трапеции равна 1,5*√2 см.

Відповідь:
60 см.
Пояснення:
Дано: КМРТ - ромб, КР=15 см, ∠К/∠Т=2:1.
Знайти периметр КМРТ.
Периметр - сума усіх сторін.
Нехай ∠Т=х°, тоді ∠К = 2х°.
Діагональ ромба ділить його кути навпіл, отже, ∠МКР=∠ТКР=2х:2=х°.
∠Р=∠К як протилежні кути ромба, отже ∠МРК=∠ТРК=х°.
Маємо ΔКРТ, де всі кути рівні, отже, і всі сторони рівні.
КР=15 см, КТ=15 см, РТ=15 см.
Всі сторони ромба рівні.
Знайдемо периметр Р
Р=15*4=60 см.