Строну параллелограмма равны 12 см и 18 см. высота, проведённая к меньшей стороне равна 9 см. вычислите длину высоты, проведённой к большей стороне параллелограмма 1)вычислим площадь параллелограмма: 2)вычислим длину искомой высоты. запишем формулу для вычисления площади параллелограмма, которая содержит искомую высоту . получим уравнение ,решим его:

👇

Ответ:

tskripko

05.03.2020

Площадь параллелограмма равна произведению длины стороны на длину проведённой к ней высоты - S=a*h. Зная, что к стороне, равной 12, проведена высота, равная 9, получим, что площадь равна 12*9=108см².

Теперь, чтобы найти длину второй высоты, подставим в формулу площади S=108 и a=18 (длина большей стороны). Получим уравнение 108=18h, откуда h=6.

ответ: h=6 см.

4,6(14 оценок)

Открыть все ответы

Ответ:

bamnames

05.03.2020

1. Найдем уравнения плоскостей АВС и АВD.
Для составления уравнения плоскости используем формулу:

|x - xA xB - xA xC - xA|
|y - yA yB - yA yC - yA| = 0.
|z - zA zB - zA zC - zA|

Подставим данные трех наших точек плоскости АВС:
|x-8 2-8 2-8|               |x-8 -6 -6|
|y-9 1-9 3-9| = 0. Или |y-9 -8 -6| = 0.
|z-6 7-6 8-6|             |z-6 1 2|
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
       |-8 -6|        |-6 -6|      |-6 -6|
(х-8)*| 1 2| - (y-9)* | 1 2| +(z-6)*|-8 -6| =0. Отсюда

(х-8)(-16+6)-(y-9)(-12+6)+(z-6)(36-48)=0. Или
-10x+6y-12z+46=0.
5x-3y+6z-23=0 - общее уравнение плоскости АВС с коэффициентами
А=5, В=-3, С=6, D=-23.

Подставим данные трех наших точек плоскости АВD:
|x-8 2-8 7-8|         |x-8 -6 -1|
|y-9 1-9 6-9| = 0. Или |y-9 -8 -3| = 0.
|z-6 7-6 1-6|           |z-6 1 -5|
Раскрываем определитель по первому столбцу, находим уравнение плоскости ABD :
     |-8 -3|        |-6 -1|         |-6 -1|
(х-8)*| 1 -5| - (y-9)*| 1 -5| +(z-6)*|-8 -3| =0.

(х-8)(40+3)-(y-9)(30+1)+(z-6)(18-8)=0.
43x-31y+10z-125=0 - общее уравнение плоскости АВD с коэффициентами
А=43, В=-31, С=10, D=-125.
Угол между плоскостями определяем по формуле:
Cosα=|A1*A2+B1B2+C1C2|/(√(A1²+B1²+C1²)*√(A2²+B2²+C2²) или
Cosα=|215+93+60|/(√(25+9+36)*√(43²+31²+10²)= 368/451=0,816.
Угол равен ≈35,3°.

2. Уравнение прямой АВ по двум точкам:
(x-1)/(4-1)=(y-6)/(5-6) или
-x+1=3y-18 или y= (-1/3)*x+19/3
y= (-1/3)*x+19/3 (уравнение прямой с угловым коэффициентом).
Угловой коэффициент k1=-1/3 (условие перпендикулярности прямых: k2=-(1/k1).
Точка С(2;-2).
Уравнение прямой, перпендикулярной прямой АВ, проходящей через точку С : Y-Yc=3*(X-Xc). Подставляем наши значения:
Y+2=3*(X-2) или 3Х-Y-8=0. - уравнение прямой Р.
Координаты точки пересечения прямых АВ и Р найдем, решив систему уравнений этих прямых:
АВ: х+3y=19 и
P: 3x-y=8. Отсюда
х=4,3
y=4,9
ответ: К(4,3;4,9).

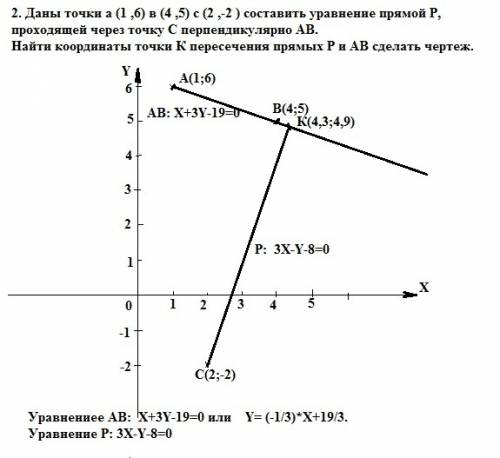
100 ! даны вершины пирамиды a(8,9,6) b(2,1,7) c(2,3,8) d(7,6,1) найти угол между гранями abc и abd.

100 ! даны вершины пирамиды a(8,9,6) b(2,1,7) c(2,3,8) d(7,6,1) найти угол между гранями abc и abd.

4,4(56 оценок)

Ответ:

tat321

05.03.2020

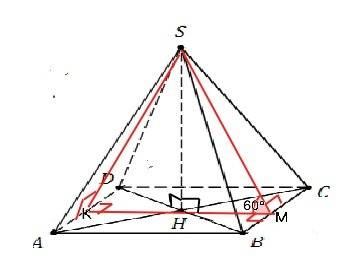
В основании правильной пирамиды - правильный многоугольник (здесь - квадрат), вершина высоты проецируется в его центр. Величина двугранного угла при ребре основания - угол между апофемой и прямой, проведенной через основание высоты параллельно одной из сторон ( обе перпендикулярны ребру в одной точке). Осевое сечение этой пирамиды - правильный треугольник ( углы при основании равны 60°), поэтому сторона основания равна основанию этого правильного треугольника. АВ=КМ=SM=10 см Ѕ(ABCD)=10²=100 см²