ответ: ВМ=22
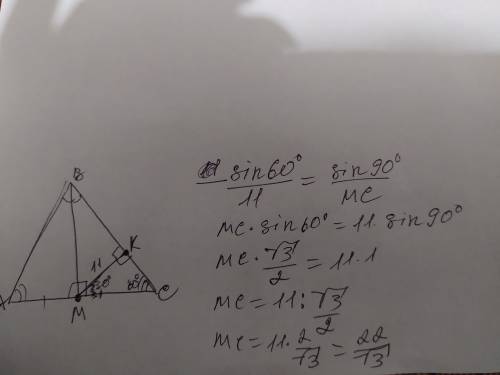
Объяснение: обозначим прямую от точки М до стороны ВС - МК=11 высотой стороны ВС. У нас получился прямоугольный треугольник МСК, в котором угол С =60°(по условиям, поскольку ∆АВС равносторонний). В ∆МСК угол СМК=30°(180-90-60). Теперь применим теорему синусов и найдём сторону МС: теорема синусов на фото ниже
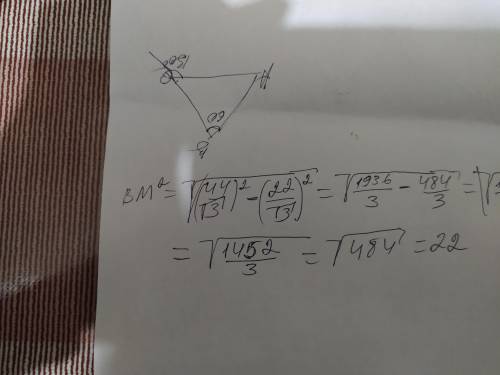
В ∆СВМ угол СВМ=30°(по условиям, поскольку медиана проведённая из вершины В является ещё биссектрисой, которая делит угол пополам и высотой. В прямоугольном ∆СВМ сторона ВС=22/√3×2=44√3(по свойствам угла 30°- катет, лежащий напротив угла 30°=половине гипотенузы). Теперь по теореме Пифагора ВМ= решение по теореме Пифагора на фото ниже
ответ: ВМ=22
Объяснение: обозначим прямую от точки М до стороны ВС - МК=11 высотой стороны ВС. У нас получился прямоугольный треугольник МСК, в котором угол С =60°(по условиям, поскольку ∆АВС равносторонний). В ∆МСК угол СМК=30°(180-90-60). Теперь применим теорему синусов и найдём сторону МС: теорема синусов на фото ниже
В ∆СВМ угол СВМ=30°(по условиям, поскольку медиана проведённая из вершины В является ещё биссектрисой, которая делит угол пополам и высотой. В прямоугольном ∆СВМ сторона ВС=22/√3×2=44√3(по свойствам угла 30°- катет, лежащий напротив угла 30°=половине гипотенузы). Теперь по теореме Пифагора ВМ= решение по теореме Пифагора на фото ниже


По условию AK и BK равны, так как точки A и B равноудалены от K - середины противоположной стороны.Следовательно треугольник AKB равнобедренный.
Проведем высоту NK из вершины K, на основание AB, NK - средняя линия четырехугольника ABCD. Так как NK является высотой то четырехугольник ABCD является прямоугольником.