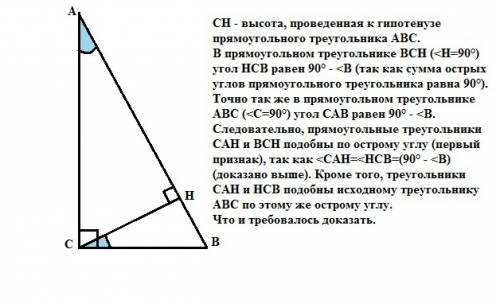
СН - высота, проведенная к гипотенузе прямоугольного треугольника АВС. В прямоугольном треугольнике ВСН (<H=90°) угол НСВ равен 90° - <B (так как сумма острых углов прямоугольного треугольника равна 90°). Точно так же в прямоугольном треугольнике АВС (<С=90°) угол САВ равен 90° - <B. Следовательно, прямоугольные треугольники САН и ВСН подобны по острому углу (первый признак), так как <CAH=<HCB=(90° - <B) (доказано выше). Кроме того, треугольники САН и НСВ подобны исходному треугольнику АВС по этому же острому углу.
Что и требовалось доказать.
Пусть наши плоскости пересекаются по прямой а. Т.е. на этой прямой будут лежать все общие точки этих плоскостей. Т.к. прямая с пересекает альфа в точке С, то эта точка лежит на прямой а, аналогично для D.
Получается что наша прямая а проходит через точки С и D. Это значит наши плоскости пересекаются по прямой CD