На сторонах угла∡ABC точки A и C находятся в равных расстояниях от вершины угла BA=BC. Через эти точки к сторонам угла проведены перпендикуляры AE⊥BA CD⊥BC.
1. Чтобы доказать равенство ΔAFD и ΔCFE, докажем, что ΔBAE и ΔBCD, по второму признаку равенства треугольников:
BA=BC
∡BAF=∡BCF=90°
∡ABC — общий.
В этих треугольниках равны все соответсвующие эелементы, в том числе BD=BE, ∡D=∡E.
Если BD=BE и BA=BC, то BD−BA=BE−BC, то есть AD=CE.
Очевидно равенство ΔAFD и ΔCFE также доказываем по второму признаку равенства треугольников:
AD=CE
∡DAF=∡ECF=90°
∡D=∡
Подробнее - на -
Объяснение:
BD = 45
CD = 32
Объяснение:
(см картинку из вопроса)
Точки D O C Образуют плоскость γ.
Прямая а содержится в плоскости γ (т.к. (·) O и C принадлежат плоскости γ).
Аналогично b ⊂ γ
A ∈ γ т.к. A ∈ a, a ⊂ γ
B ∈ γ т.к. B ∈ b, b ⊂ γ
AB ⊂ γ
AB одновременно принадлежит α и γ значит прямая AB является линией пересечения α и γ
Аналогично DC является линией пересечения β и γ
α || β, α,β ∩ γ ⇒ AB || DC (линии пересечения параллельны)
(смотри мою картинку)
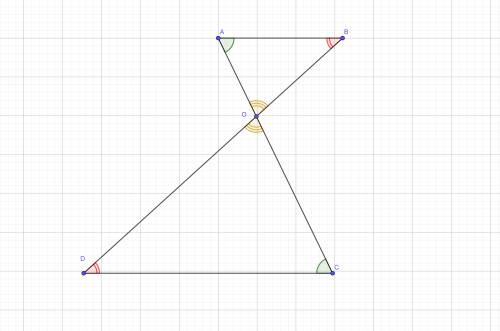
Рассмотрим плоскость γ
Зеленые углы равны как накрестлежащие при параллельных прямых.
Красные углы тоже равны как накрестлежащие.
Желтые углы равны как вертикальные.
Треугольники OAB и OCD подобны по двум углам.
Значит 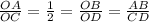
Следовательно 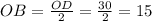
BD = OD + OB = 30 + 15 = 45
Следовательно CD = AB * 2 = 16 * 2 = 32
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!
Р = 26 · 2 + 15 = 52 + 15 = 67 см
2. Углы при основании равнобедренного треугольника равны.
Тогда найдем угол при вершине:
180° - 2·45° = 90°
ответ: 45°, 45°, 90°