Вступление:
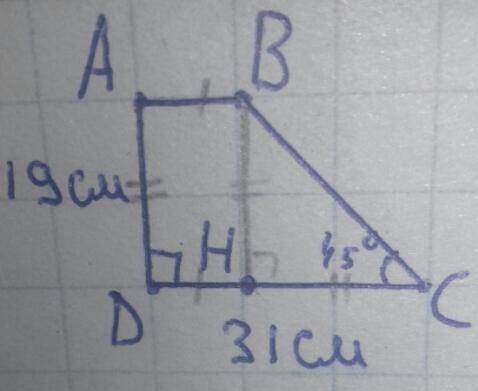
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
Полупериметр равен 11, т.е. сумма сторон равна 11, а произведение 28, это 7 и 4. Но для порядка) составим квадратное уравнение, помня, что его корни могут для нас быть только положительными числами. Пусть одна сторона х, тогда смежная ей 11- х, составим и решим уравнение.х*(11-х)=28. Раскроем скобки. 11х-х²=28, Упростим. х²-11х+28, по теореме, обратной теореме Виета, угадаем корни. Это 7 и 4, т.е. если одна сторона 7, то вторая 11-7=4, а если одна сторона 4, то другая 11-4=7. Итак, стороны прямоугольника 7см, 4см, 7см, 4см.