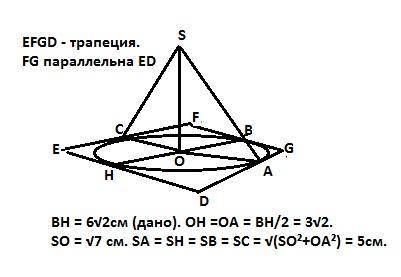
Расстояние от точки S до сторон трапеции равно 5 см.
Объяснение:
Расстояние от точки S до сторон трапеции - это перпендикуляры, проведенные из этой точки к сторонам. Опустим перпендикуляр SO на плоскость трапеции и соединим точку О с концами перпендикуляров от точки S до сторон. По теореме о трех перпендикулярах проекции расстояния от точки S до сторон перпендикулярны сторонам трапеции. Если наклонные (расстояния от S до сторон) равны, то равны и их проекции. Следовательно, точка S проецируется в центр вписанной в трапецию окружности, радиус которой равен половине высоты трапеции, то есть
R = 3√2 см.
Расстояние от точки S до сторон трапеции - это гипотенуза прямоугольного треугольника с катетами - √7 см и 3√2 см.
По Пифагору: L = √(7+18) = 5 cм.
2) тр А1ВС1 подобен тр А2ВС2 ( по двум углам), а именно
уг А - общий
уг ВА1С1 = ВА2С2 как сjответственные при A1C1||A2C2 и секущ ВА2
⇒А1В / А2В = С1В/ С2В = k
k= 1/4
BC1 / BC2 = 1/4
BC1 / 12 = 1/4
BC1 = 3