Расстояние между параллельными прямыми есть длина перпендикулярного этим прямым отрезка, заключенного между ними.
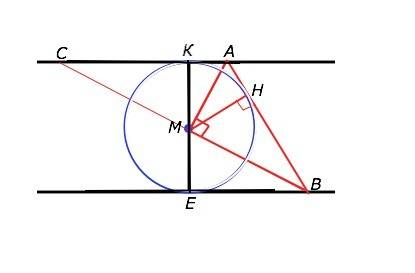
Обозначим данные прямые а и b. Отрезок КЕ ⊥ а, КЕ ⊥ b.
М - середина КЕ, КМ=МЕ=50. Угол АМВ=90°.
Продолжим ВМ до пересечения с прямой а в точке С.
∆КМС =∆ВМЕ по катетам КМ=МЕ и вертикальным углам при М. Смежные углы АМВ=АМС=90°,АМ - высота и медиана ∆ САВ, ⇒,
АМ - биссектриса угла ВАС.
Каждая точка биссектрисы равноудалена от сторон угла. МК=МН, где МН - расстояние от М до АВ.
М - центр вписанной в угол САВ окружности с диаметром, равным расстоянию между параллельными а и b.
Наименьшее расстояние от точки до прямой – перпендикуляр, и наименьшим расстоянием от М до АВ будет радиус МН=МК окружности с диаметром КЕ=100, т.е. отрезок, равный половине КЕ:2=50 (ед. длины).
В четырёхугольнике АОСД ∠АОС+∠АДС=360-(∠ОАД+∠ОСД)=360-(90+90)=180°.
В четырёхугольнике АОСД суммы противолежащих углов равны, значит он вписанный.
доказано.
б) АО⊥АВ и ВО1⊥АВ, значит АО║ВО, значит ∠АОО1+∠ВО1О=180°.
АО=СО, АД=СД, значит ΔАДО=ΔСДО, значит ДО - биссектриса угла АОС.
Аналогично ДО1 - биссектриса угла ВО1С.
ДО и ДО1 биссектрисы односторонних углов, значит ∠ОДО1=90°.
В тр-ке ОО1Д ДС²=ОС·О1С=3·5=15.
В тр-ке СОД ОД=√(ОС²+ДС²)=√(9+15)=√24=2√6.
В тр-ке СОД радиус описанной окружности равен половине гипотенузы.
R=ОД/2=√6 - это ответ.
Действительно, радиус описанной окружности около четырёхугольника равен радиусу описанной окружности вокруг любого из треугольников, образованных из его вершин.