Объяснение:
Дана правильная треугольная пирамида. Её высота Н равна a√3, радиус окружности, описанной около её основания, равен 2a.
Найти: а) апофему А пирамиды.
Радиус R окружности, описанной около её основания, равен 2/3 высоты основания, то есть R = в√3/3, где в - сторона основания.
Находим сторону основания: в = R/(√3/3) = R√3 = 2a√3.
Отсюда апофема равна: А = √(Н² + (R/2)²) = √(3a² + a²) = √4a² = 2a.
Величина R/2 равна 1/3 высоты основания или радиусу вписанной окружности в основание.
б) угол α между боковой гранью и основанием равен:
α = arc tg(H/(R/2)) = arc tg(a√3/a) = arc tg√3 = 60 градусов.
в) площадь Sбок боковой поверхности.
Периметр основания Р = 3в = 3*2a√3 = 6a√3.
Sбок = (1/2)РА = (1/2)*(6a√3)*2а = 6a²√3 кв.ед.
г) плоский угол γ при вершине пирамиды(угол боковой грани).
γ = 2arc tg((в/2)/А) = 2arc tg((2а√3/2)/2а) = 2arc tg(√3/2) ≈ 1,42745 радиан или 81,7868 градуса.
y' = 12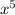 + sinx
+ sinx
Объяснение:
Для нахождения производной, воспользуемся двумя формулами:
1) при нахождении производной разности, нужно помнить, что производная разности равна разности производных. (u - v)' = u' - v'. Если немного запутано, то когда будешь смотреть пример, то, думаю, поймёшь. 2) (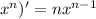 3) (cosx)' = - sinx
3) (cosx)' = - sinx
у = 2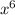 - cosx
- cosx
y' = (2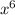 - cosx)' = (2 ·
- cosx)' = (2 · 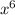 )' - (cosx)' = 2 · (
)' - (cosx)' = 2 · (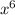 )' - (cosx)' = 2 · 6
)' - (cosx)' = 2 · 6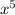 - (-sinx) = 12
- (-sinx) = 12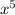 + sinx
+ sinx
Попробую ещё немного объяснить:
Как получить производную от 2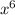
Сначала перепишем за знак производной константу 2 (2 - число, которое не может просто взять и измениться само по себе - константа) и поставим знак умножения, дальше нас интересует нахождение производной от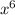 . По формуле, которую я записала выше, мы можем увидеть, что показатель степени 6 мы записываем перед х (становится множителем), но х не остаётся без показателя степени, по формуле записано n - 1, то есть в нашем случае это 6 - 1 ( = 5), то есть х становится в 5й степени.
. По формуле, которую я записала выше, мы можем увидеть, что показатель степени 6 мы записываем перед х (становится множителем), но х не остаётся без показателя степени, по формуле записано n - 1, то есть в нашем случае это 6 - 1 ( = 5), то есть х становится в 5й степени.
С косинусом даже легче: производная косинуса (по формуле) равна синусу, но обязательно со знаком минус, т.е. - sinx
Третий момент, на который нужно обратить внимание, - то, что перед косинусом первоначально был минус. При нахождении производной получается - (-sinx), если перед скобкой стоит минус, то знак в скобках меняется, поэтому в ответе становится + sinx.
Если ещё есть вопросы, задавай в комментариях.