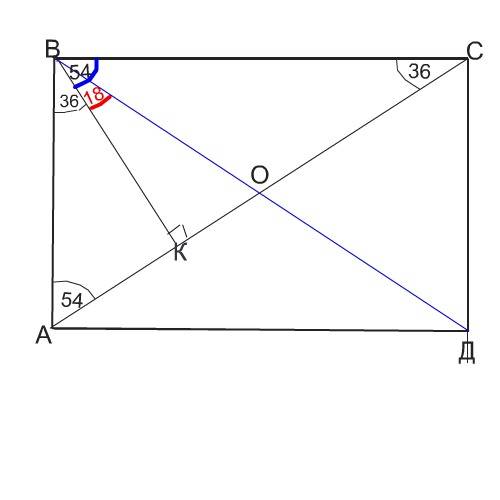
Обозначим для удобства этот прямоугольник АВСД.
Пересечение перпендикуляра из В с диагональю обозначим К.
Если отношение углов, на которые делится прямой угол, равно 2:3, значит, этот угол разделен на 5 частей, 2 из которых принадлежат одному углу, 3 - другому.
90:(2+3)=18°
Угол АВК равен 18*2=36°
Угол СВК равен 18*3=54°
Треугольник ВКС - прямоугольный.
Т.к. угол СВК=54°,
угол ВСА равен 90-54=36°
1) углы, образованные диагоналями со сторонами примоугольника, равны 36° и 54°
---------------------------------------------
Рассматриваем рисунок, чтобы найти ответ на второй вопрос задачи.
Треугоьлник ВОС - равнобедренный по свойству диагоналей прямоугольника, которые равны и точкой пересечения делятся пополам.
Следовательно, угол ОВС равен 36° , а угол КВО, который перпендикуляр КВ образовал с диагональю ВД, равен 54-36=18°
2) ответ на второй вопрос задачи:
Этот угол равен 18°
-------------
Примечание: При решении можно использовать свойство углов при пересечении двух параллельных прямых секущей. Я выбрала решение через треугольники.
АД И ВС - ПАРАЛЛЕЛЬНЫЕ ОСНОВАНИЯ ТРАПЕЦИИ АВСД, БИССЕКТРИСЫ АО И ВО ПЕРЕСЕКАЮТСЯ В ТОЧКЕ О И ПРОХОДЯТ ДАЛЬШЕ, ПЕРЕСЕКАЯ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ТОЧКАХ А1 И В1. УГЛЫ ВА1А И А1АВ1 - ВНУТРЕННИЕ РАЗНОСТОРОННИЕ ПРИ ПАРАЛЛЕЛЬНЫХ ВС И АД И СЕКУЩЕЙ АА1 . РАССМОТРИМ ТРЕУГОЛЬНИК АВА1. В НЕМ УГЛЫ ВАА1 И ВА1А РАВНЫ, Т.К. АА1- БИССЕКТРИСА УГЛА ВАД, ТРЕУГОЛЬНИК АВА1 РАВНОБЕДРЕННЫЙ, ЕГО БИССЕКТРИСА, ОПУЩЕННАЯ НА ОСНОВАНИЕ, ЯВЛЯЕТСЯ ВЫСОТОЙ (И МЕДИАНОЙ ПО СВОЙСТВУ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА) УГОЛ АОВ = 90 ГРАД.
а=P:4=68:4=17
x*y/2=240⇒x*y=480
(x/2)²+(y/2)²=a²⇒x²+y²=1156
x=480/y
(480/y)²+y²=1156
y^4-1156y²+230400=0
y²=z
z²-1156z+230400=0
D=1336336-921600=414736 √D=644
z1=(1156-644)/2=256⇒y²=256
y1=16⇒x1=480/16=30
y2=-16-не удов усл
диагонали ромба 16 и 30